快速排序实现及优化

Algorithm


本文将介绍从一路快速排序，二路快速排序，三路快速排序一步步实现以及优化的过程

Quick Sort 基本思想

基本思想：每次从当前待排序序列中选取一个元素作为基准(pivot)，如下图所示，这里我们选取的元素是4，之后想办法把4(基准)挪到整个序列排好序时应该所处的位置，此时4(基准)之前的元素是小于4的，4之后的元素是大于4的，对小于4(基准)的序列和大于4(基准)的序列分别使用快速排序逐渐递归下去，完成整个排序过程。

原理

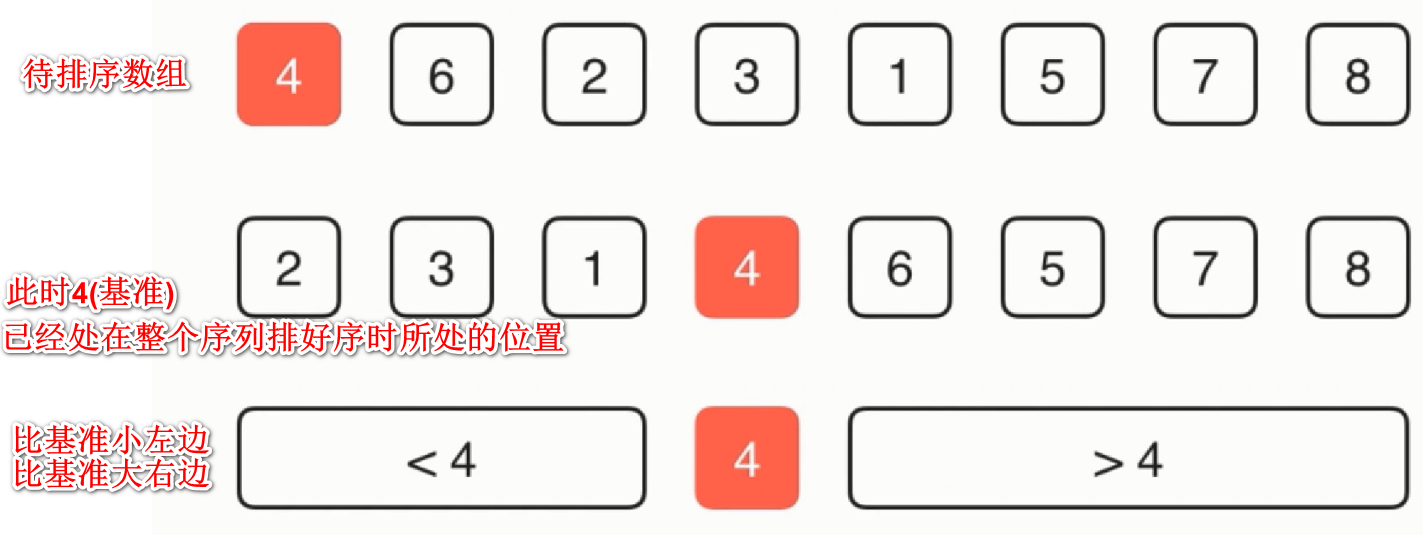
一路快速排序图片相关参数介绍：

  • v: 基准
  • l: 也就是left
  • r: 也就是right
  • i: 当前访问的元素
  • j: 记录大于v(基准)小于v的分界点，指向<v的最后一个元素

一路快速排序 原理演示

将把序列分成两个部分的过程称为Partition,一般将数组的第一个元素作为基准（基准的选取影响了整个程序的效率，有三种选取方法），从left + 1 位置开始遍历序列，将序列分成小于v的部分和大于v的部分

原理

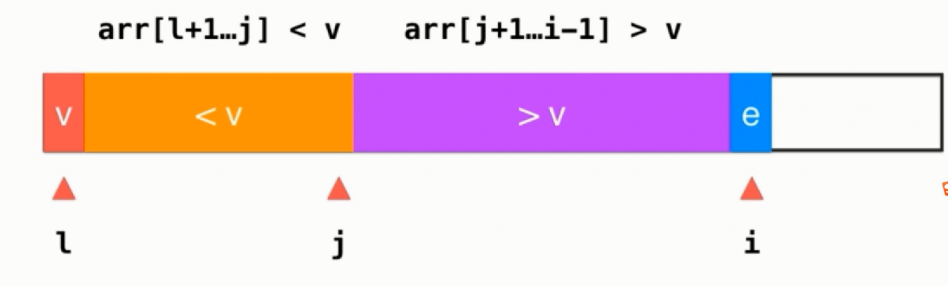
arr[left+1 ... j] < v 这段左闭右闭的区间是小于v的，arr[j+1 ... i-1] > v这段左闭右闭的区间是大于v的，如果当前所指向元素arr[i] > v，则i++,动画演示如下：

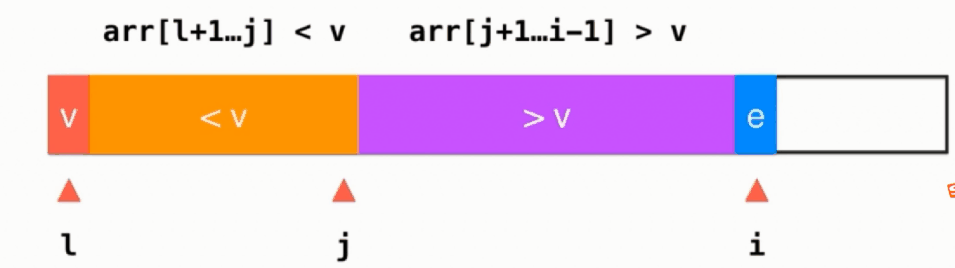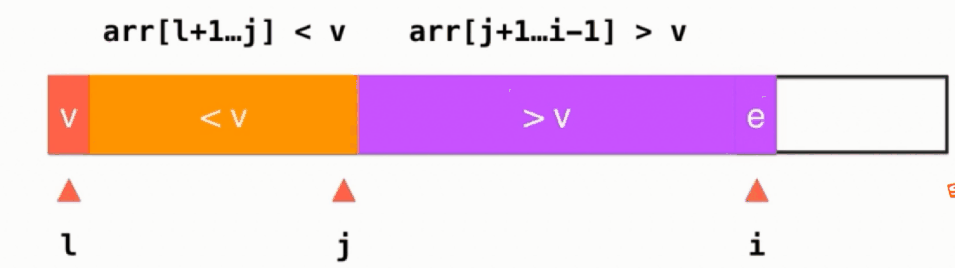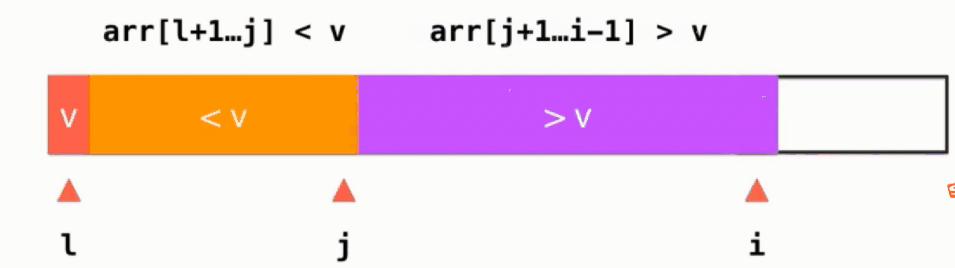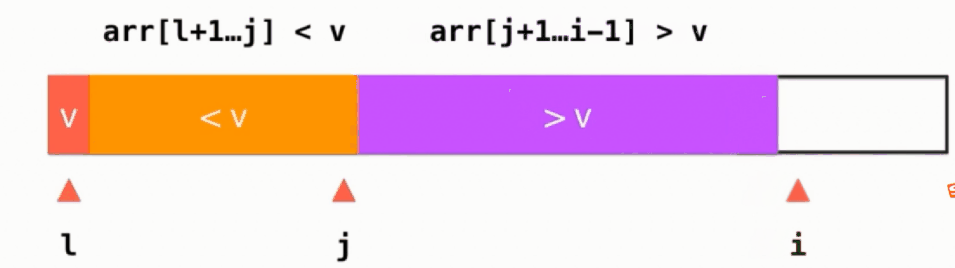
如果当前所指元素arr[i] < v，则swap(arr[i], arr[j+1]), 并且j++, i++,动画演示如下:

遍历完整个序列是这样子的：

最后要将v放到它应该在的位置,即swap(arr[left],arr[j])，动画演示如下：

一路快速排序 代码实现

为了方便从数组描述算法的性能，我把一些辅助函数放在SortHelper.h的头文件里，内容如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
#ifndef ALGORITHM_SORTHELP_H
#define ALGORITHM_SORTHELP_H
#include <stdlib.h>
#include <time.h>

// 生成有n个元素的随机数组,每个元素的随机范围为[rangeL, rangeR] 左闭右闭区间
int * generateRandomArray(int n, int rangeL, int rangeR)
{
    int i;
    int *arr = NULL;
    if (n > 0 && rangeR >= rangeL)
    {
        arr = (int *) malloc(sizeof(int) * n);   // 用malloc 分配数组 是因为不用malloc的话 随着此函数的结束 数组空间会被释放掉
        srand(time(NULL));                       // 设置随机种子
        for (i = 0; i < n; ++i)
        {
            arr[i] = rand() % (rangeR - rangeL + 1) + rangeL;  // 注意随机数所在区间区间是[rangeL, rangeR]
        }
    }
    return arr;
}

// 交换两个数
void swap(int * a, int * b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}

// 生成近乎有序的数组  n:数据个数  swapTimes:交换次数  最多只有2*交换次数个元素无序
int * generateNearlyOrderArray(int n, int swapTimes)
{
    int i;
    int *arr = NULL;
    if (n > 0 && swapTimes >= 0)
    {
        arr = (int *) malloc(sizeof(int) * n);
        srand(time(NULL));

        for (i = 0; i < n; ++i)
        {
            arr[i] = i;
        }

        for (i = 0; i < swapTimes; ++i)
        {
            int x = rand() % n;
            int y = rand() % n;
            swap(&arr[x], &arr[y]);
        }
    }
    return arr;
}

// 测试此排序方法 第四个形参传递的是方法
void testSort(int * arr, int n, char * sortName , void(*sort)(int * , int ))
{
    clock_t startTime = clock();
    sort(arr, n);
    clock_t endTime = clock();
    printf("%s cost time: %lf s\n", sortName, (double) (endTime - startTime) / CLOCKS_PER_SEC);
}

// 复制数组
int * copyArray(int * arr, int n)
{
    int i;
    int *newArr = (int *) malloc(sizeof(int) * n);
    for (i = 0; i < n; ++i)
    {
        newArr[i] = arr[i];
    }
    return newArr;
}

// 插入排序
void InsertionSort(int * arr, int left, int right)
{
    int i, j;
    for (i = left + 1; i <= right; ++i)
    {
        int temp = arr[i];
        for (j = i; j > left && arr[j-1] > temp; j--)
        {
            arr[j] = arr[j - 1];
        }
        arr[j] = temp;
    }
}

// 打印数组内容
void printArray(int * arr, int n)
{
    int i;
    for (i = 0; i < n; ++i)
    {
        printf("%d  ", arr[i]);
    }
    printf("\n");
}
#endif //ALGORITHM_SORTHELP_H

QuickSortOneWays.c源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <stdio.h>
#include <stdlib.h>
#include "SortHelp.h"

// 对arr[left...right]部分进行partition操作
// 返回posi,使得arr[left...p-1] < arr[p] ; arr[p+1...right] > arr[p]
int __partition(int *arr, int left, int right)
{
    int i, j;
    int v = arr[left];                      // 基准
    j = left;
    for (i = left + 1; i <= right; ++i)
    {
        // 如果当前元素 比 基准小
        if (arr[i] < v)
        {
            swap(&arr[i], &arr[j + 1]);
            j++;
        }
        // 比基准大 i++
    }
    swap(&arr[left], &arr[j]);
    return j;
}

// 对arr[left, right]进行快速排序
void __QuickSortOneWays(int * arr, int left, int right)
{
    if (left >= right)                          // 递归结束条件
    {
        return;
    }
    int p = __partition(arr, left, right);      // 排好序后 基准所在位置的索引
    __QuickSortOneWays(arr, left, p - 1);              // 对左子序列进行快排
    __QuickSortOneWays(arr, p + 1, right);             // 对右子序列进行快排
}

// 统一接口
void QuickSortOneWays(int * arr, int n)
{
    __QuickSortOneWays(arr, 0, n - 1);
}


int main(void)
{
    // 生成随机数组测试
    int n = 100000;
    int *arr = generateRandomArray(n, 0, n);    // 生成n个[0,n]的随机数
    testSort(arr, n, "QuickSortOneWays", QuickSortOneWays);
    // printArray(arr, n);

    // 生成 几乎有序的数组 最多只有2*100个元素无序
    int swapTimes = 100;
    int *arr1 = generateNearlyOrderArray(n, swapTimes);
    testSort(arr1, n, "QuickSortOneWays", QuickSortOneWays);
    // printArray(arr1, n);

    // 生成大量重复元素数组 [0,10]
    int *arr2 = generateRandomArray(n, 0, 10);
    testSort(arr2, n, "QuickSortOneWays", QuickSortOneWays);
    // printArray(arr2, n);
    return 0;
}

Clion运行结果如下：

可以看出一路快速排序的缺点在有大量重复元素，近乎有序的序列,运行效率都非常慢,二路快速排序由此被引伸出来,在此一路快速排序还有两个地方可以优化：

  1. 当规模小于某个值时 使用插入排序
  2. 基准的选取 这里采用随机数法 三位取中法 更好一点 因为rand() 需要时间

基准选取的三种方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
/** 三数取中法  **/
int mid = left + (right - left) / 2;
// 这里取三个数排序后，中间那个数作为枢轴
if (arr[left] > arr[mid])
{
    swap(&arr[left], &arr[mid]);
}
if (arr[left] > arr[right])
{
    swap(&arr[left], &arr[right]);
}
if (arr[mid] > arr[right])
{
    swap(&arr[mid], &arr[right]);
}
/* 此时 arr[left] <= arr[mid] <= arr[right]*/
swap(&arr[left], &arr[mid]);    // 将基准放到最左边
int v = arr[left];

/** 随机选取 **/
swap(&arr[left], &arr[rand() % (right - left + 1) + left]);   // 选取随机基准 与arr[left]交换
int v = arr[left];                                            // 基准 此时基准已经时交换了的随机数

/** 固定基准 **/
int v = arr[left];

优化之后的源代码QuickSortOneWays1.c：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "SortHelp.h"

// 对arr[left...right]部分进行partition操作
// 返回posi,使得arr[left...p-1] < arr[p] ; arr[p+1...right] > arr[p]
int __partition1(int *arr, int left, int right)
{
    int i, j;
    /******************* 优化2 *******************/
    swap(&arr[left], &arr[rand() % (right - left + 1) + left]);

    int v = arr[left];                      // 基准
    j = left;
    for (i = left + 1; i <= right; ++i)
    {
        // 如果当前元素 比 基准小
        if (arr[i] < v)
        {
            swap(&arr[i], &arr[j + 1]);
            j++;
        }
        // 比基准大 i++
    }
    swap(&arr[left], &arr[j]);
    return j;
}


// 对arr[left, right]进行快速排序
void __QuickSortOneWays1(int * arr, int left, int right)
{
    /************ 优化1 **********/
    if (right - left <= 15)                      // 递归结束条件
    {
        InsertionSort(arr, left, right);
        return;
    }
    int p = __partition1(arr, left, right);      // 排好序后 基准所在位置的索引
    __QuickSortOneWays1(arr, left, p - 1);          // 对左子序列进行快排
    __QuickSortOneWays1(arr, p + 1, right);         // 对右子序列进行快排
}

// 统一接口
void QuickSortOneWays1(int * arr, int n)
{
    srand(time(NULL));
    __QuickSortOneWays1(arr, 0, n - 1);
}

int main(void)
{
    // 生成随机数组测试
    int n = 100000;
    int *arr = generateRandomArray(n, 0, n);    // 生成n个[0,n]的随机数
    testSort(arr, n, "QuickSortOneWays", QuickSortOneWays1);

    // 生成 几乎有序的数组 最多只有2*100个元素无序
    int swapTimes = 100;
    int *arr1 = generateNearlyOrderArray(n, swapTimes);
    testSort(arr1, n, "QuickSortOneWays", QuickSortOneWays1);

    // 生成大量重复元素数组 [0,10]
    int *arr2 = generateRandomArray(n, 0, 10);
    testSort(arr2, n, "QuickSortOneWays",QuickSortOneWays1);
    return 0;
}

优化后Clion运行结果：(数据规模100000 10万)

测试数据规模为100000(10万)，发现在几乎有序的数组中，从之前的15.284000s提高到0.022000s，效率明显高了不少（而且我们快速排序的对象只是一个数组，内部设计不是很复杂），在大量重复元素和随机数组中效率差不多，这是为什么呢？下面我用图来解释。

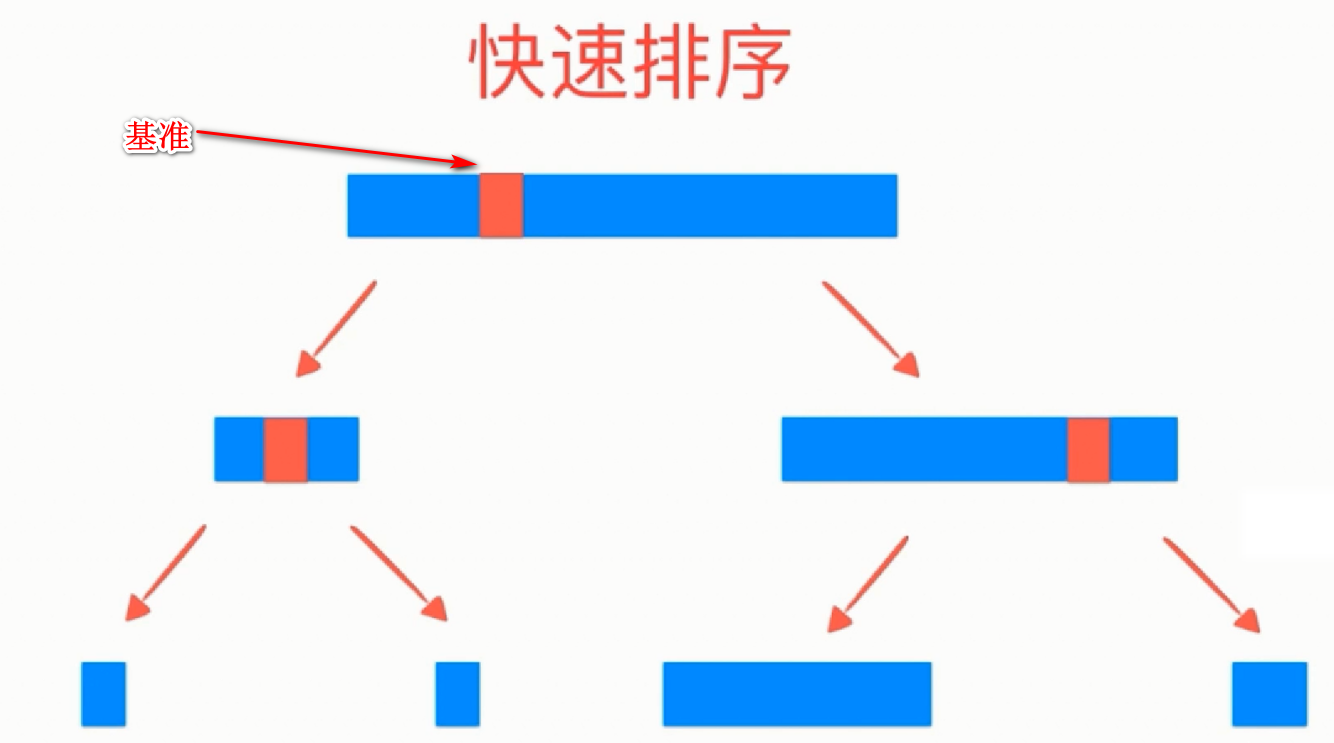
随着基准选取的不同,快速排序的效率也受到了影响，当基准能把原序列换分成均匀的两个子序列时，每一次递归层次上比较的次数都是O(N)次，而递归的深度是 log2^N (每次都是将原始序列分一半，即一直除2)，最好的情况下时间复杂度应为O(Nlog2^N),最坏的情况下，即基准每次是第一个元素，用因为是有序的，比基准小的元素没有，只有比基准大的元素，每次划分序列都近似于1和N-1，划分极度不均匀，像一个单链表，导致时间复杂度为O(N^2),最坏情况下，快速排序图解如下：

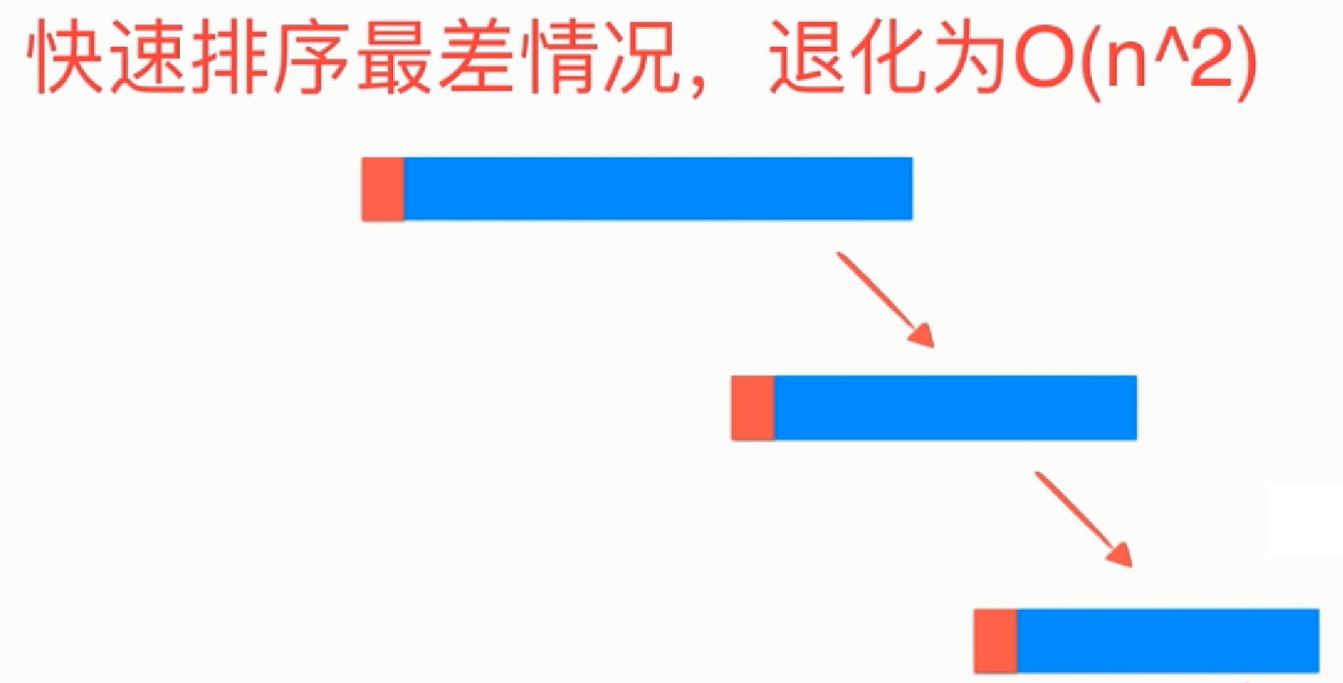
其中空间复杂度为O(log2^N)，递归的深度为log2^N，系统栈需要压入log2^N种状态，需要空间O(log2^N),在快排过程种定义的left,right…,都是常数级需要空间O(1),总共耗费空间O(log2^N) * O(1)。
这里解释下我为什么基准选取随机数：最坏的情况下，数组完全有序，每次选中最左边的元素，$ \frac{1}{n} \times \cfrac{1}{n-1} \times \cfrac{1}{n-2} \times….. \cfrac{1}{1} $ 当n无穷大时，出现最坏情况的概率接近于0

二路快速排序

当我在一路快速排序已经进行优化的代码中（基准选取得当解决了近乎有序数组的问题），把数组规模再扩大10倍（百万），Clion运行结果如下:

从数据观察到，含有大量重复元素时，快速排序算法的复杂度似乎又退化到了O(N^2)，这是因为我们之前并没有算当前元素e==v这种情况，如图：

原理

假设此时我们把e==V 放在黄色区域,或者把e==v放在紫色区域,最后都会变成这样：

原理

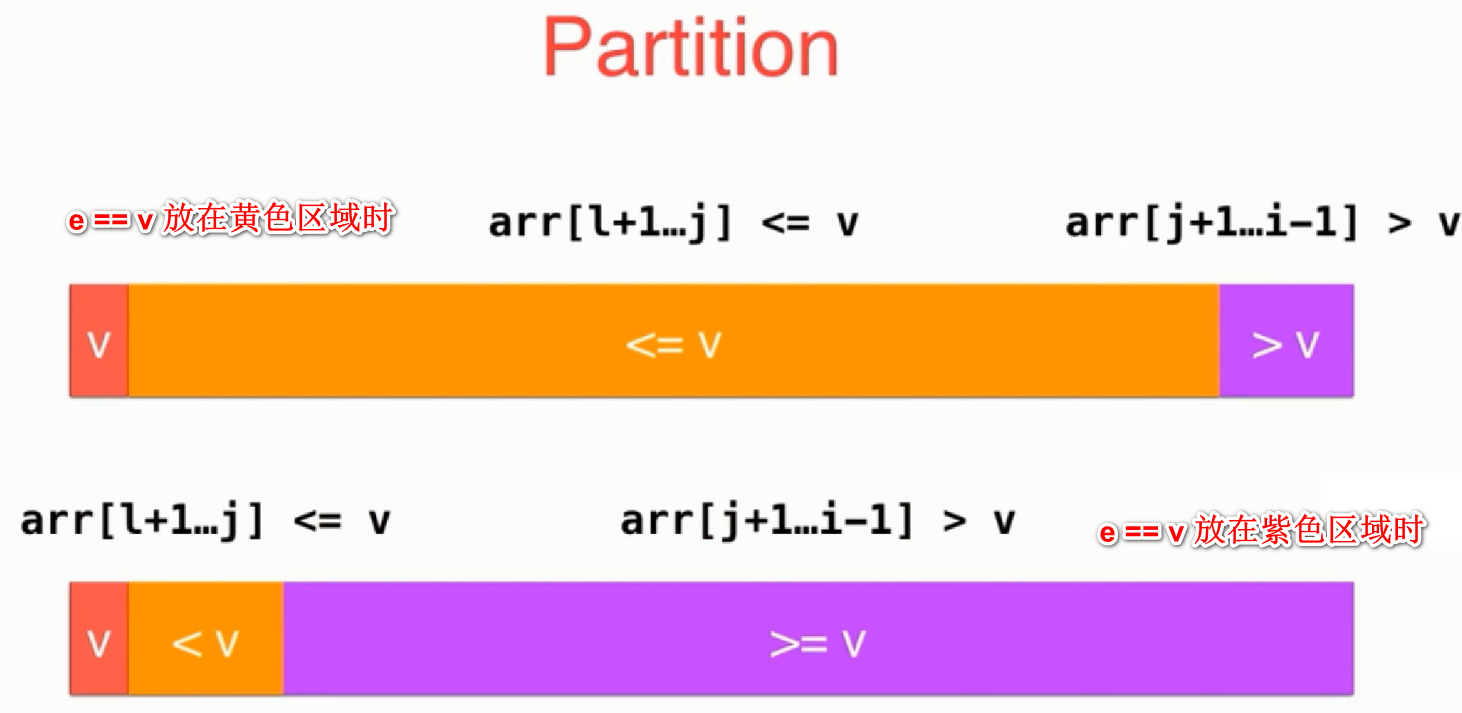
partition这个过程极有可能将序列分为极度不平衡的两个子序列，而最好的情况是划分为均匀的两个序列O(log2^N)，此时的情况更接近于最坏的情况O(N^2)， 如何解决这个问题呢？ 二路快速排序由此而来.

二路快速排序图片相关参数介绍：

  • v: 基准
  • l: 也就是left
  • r: 也就是right
  • e: 当前所指向元素
  • i: 记录小于v这一端即将要扫描的位置(向右)
  • j: 记录大于v这一端即将要扫描的位置(向左)

二路快速排序 基本思想

基本思想：首先我们从i开始向右扫描，如果当前扫描到的元素e < v 则i往后移(i++)，直到碰到当前元素e >= v停止。然后从j开始向左扫描,如果当前元素e > v，则j往前移(j--),直到遇到 e <= v，则将i,j对应的元素 交换，i++，j--，再从i开始重复此过程，直到i，j相遇，然后把基准放到j对应的位置，即swap(arr[left, arr[j])代表整个序列遍历完毕，动画如下:

实际上上面的图最后那里有点错误，正确的图如下：

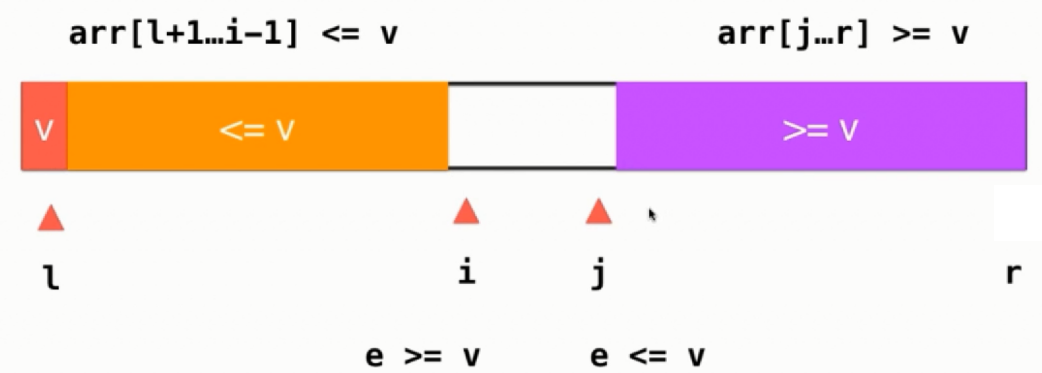
根据我们描叙的逻辑，橙色部分 <= v的元素， 紫色部分 >= v的元素,这就解决了大量重复元素集中在一个区域的情况，之前一路快速排序=v的元素，根据自己设置的代码逻辑要么集中在黄色区域，要么就是紫色区域，造成划分的子序列不均匀,现在=v即可以在黄色区域，又可以在紫色区域，换句话来说假设i,j此时都指向等于v的元素，两者还是会交换，这样就不会造成=v的元素集中在一个区域。

二路快速排序 代码实现

QuickSortTwoWays.c源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "SortHelp.h"

// 对arr[left...right]部分进行partition操作
// 返回p, 使得arr[left...p-1] < arr[p] ; arr[p+1...right] > arr[p]
int __partitionTwoWays(int *arr, int left, int right)
{
    int i, j;
    swap(&arr[left], &arr[rand() % (right - left + 1) + left]);   // 选取随机基准 与arr[left]交换
    int v = arr[left];                                            // 基准 此时基准已经时交换了的随机数

    // arr[left+1...i) <= v; arr(j...right] >= v
    i = left + 1, j = right;                                      // i初始化为left+1 刚好arr[left+1..i)无效 j同理
    while (1)
    {
        // i 从左向右扫描 遇到比基准小的元素 i++
        // 注意这里的边界, arr[i] < v, 不能是arr[i] <= v    思考一下为什么?
        while (i <= right && arr[i] < v)        // 写成i <= j 也可以
        {
            i++;
        }

        // j 从右向左扫描 遇到比基准大的元素 j--
		// 注意这里的边界, arr[j] > v, 不能是arr[j] >= v 思考？
        while (j >= left + 1 && arr[j] > v)     // 写成j >= i 也可以
        {
            j--;
        }

        // 两者相遇时 按照之前的动画逻辑  相遇时 i>j 用数据加图来体会
        if (i > j)
        {
            break;
        }
        swap(&arr[i], &arr[j]);         // i,j两者对应元素交换
        i++;
        j--;
    }
    swap(&arr[left], &arr[j]);          // 把基准放到 排好序应该在的位置 注意是与j交换不是i 画图体会
    return j;
	
/*
	比如数组 1,0,0, ..., 0, 0
	a. 对于arr[i]<v和arr[j]>v的方式，第一次partition得到的分点是数组中间；
	b. 对于arr[i]<=v和arr[j]>=v的方式，第一次partition得到的分点是数组的倒数第二个。
	这是因为对于连续出现相等的情况，a方式会交换i和j的值；而b方式则会将连续出现的这些值归为其中一方，使得两棵子树不平衡
*/
}

// 对arr[left, right]进行快速排序
void __QuickSortTwoWays(int *arr, int left, int right)
{
    if (right - left <= 15)                      // 递归结束条件
    {
        InsertionSort(arr, left, right);
        return;
    }
    int p = __partitionTwoWays(arr, left, right);      // 排好序后 基准所在位置的索引
    __QuickSortTwoWays(arr, left, p - 1);              // 对左子序列进行快排
    __QuickSortTwoWays(arr, p + 1, right);             // 对右子序列进行快排
}

// 统一接口
void QuickSortTwoWays(int *arr, int n)
{
    srand(time(NULL));
    __QuickSortTwoWays(arr, 0, n - 1);
}

int main(void)
{
    // 生成随机数组测试
    int n = 1000000;
    int *arr = generateRandomArray(n, 0, n);           // 生成n个[0,n]的随机数
    testSort(arr, n, "QuickSortTwoWays", QuickSortTwoWays);
    // printArray(arr, n);                             // 打印元素 看是否排序成功

    // 生成 几乎有序的数组 最多只有2*100个元素无序
    int swapTimes = 100;
    int *arr1 = generateNearlyOrderArray(n, swapTimes);
    testSort(arr1, n, "QuickSortTwoWays", QuickSortTwoWays);

    // 生成大量重复元素数组 [0,10]
    int *arr2 = generateRandomArray(n, 0, 10);
    testSort(arr2, n, "QuickSortTwoWays", QuickSortTwoWays);

    return 0;
}

二路快速排序Clion运行结果：(数据规模1000000 1百万)

优化后的一路快速排序Clion运行结果：(数据规模1000000 1百万万)

可以看出二路快速排序在处理随机元素， 几乎有序元素，大量重复元素, 效率都很不错,对比一路快排尤其在含大量重复元素时，优化了不少.但是对含有大量重复元素时，还有一个更好的方法，那就是下面要介绍的三路快速排序

三路快速排序

基本思想:之前二路快速排序将序列分为v两部分，现在三路快速排序将序列分为 v 三部分，这样分割之后在递归的过程中对于==v的部分，就可以不用管了，只需要对<v >v的部分进行递归排序，更有效的解决了含有大量重复元素的序列

三路快速排序图片相关参数介绍：

  • v: 基准
  • l: 也就是left
  • lt:指向<v部分的最后一个元素
  • r: 也就是right
  • e: 当前所指向元素
  • i: 当前所指向元素
  • gt:大于v部分的第一个元素

如果当前元素 e==v，直接i++，如下图所示：

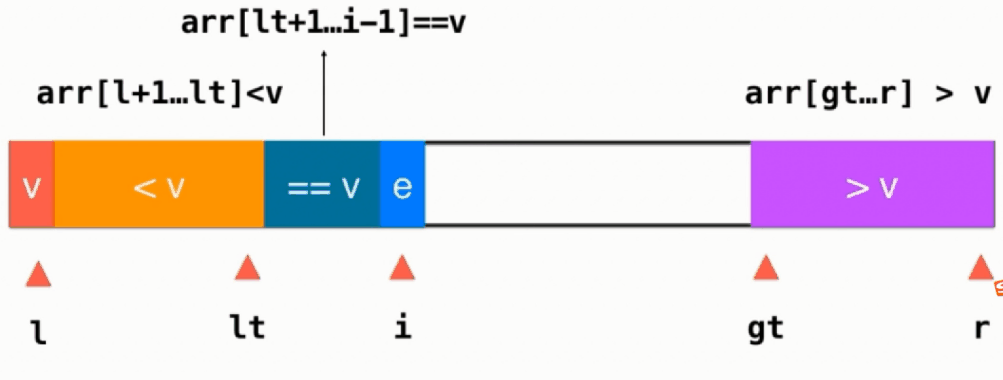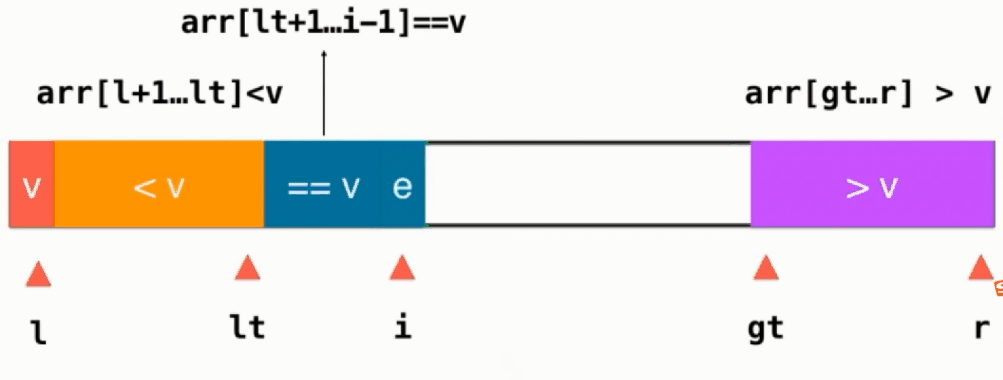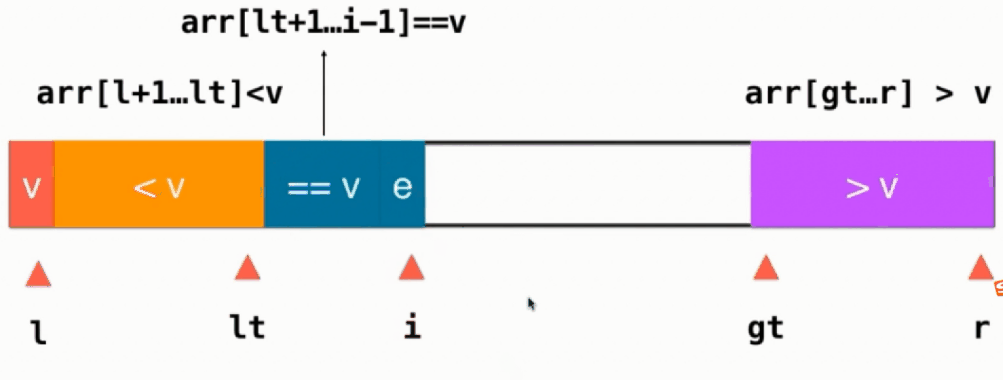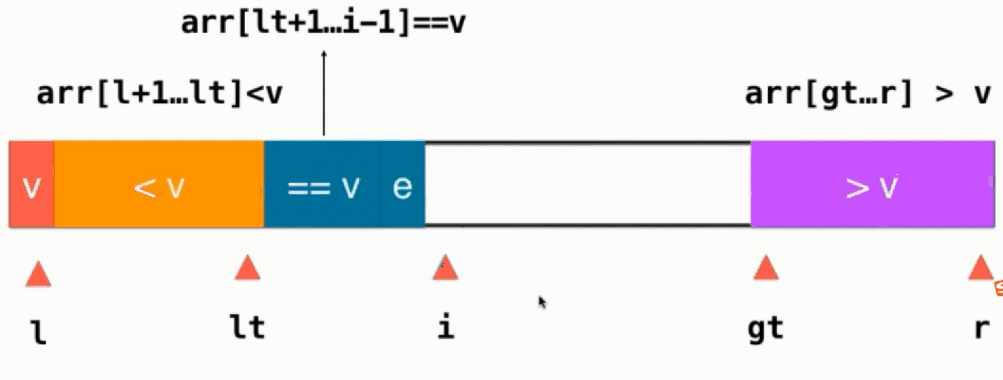
如果当前元素 e < v，则当前元素与==v部分的第一个元素交换，即swap(arr[i], arr[lt+1]),然后lt++, i往后移,i++

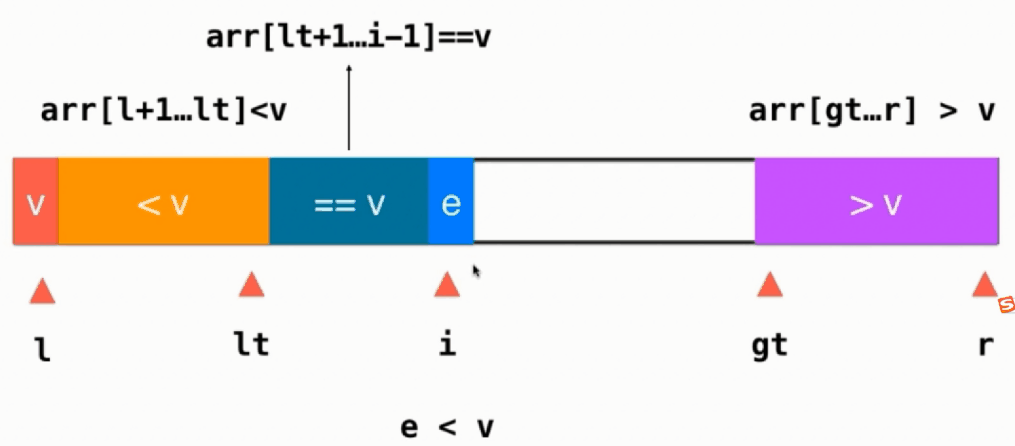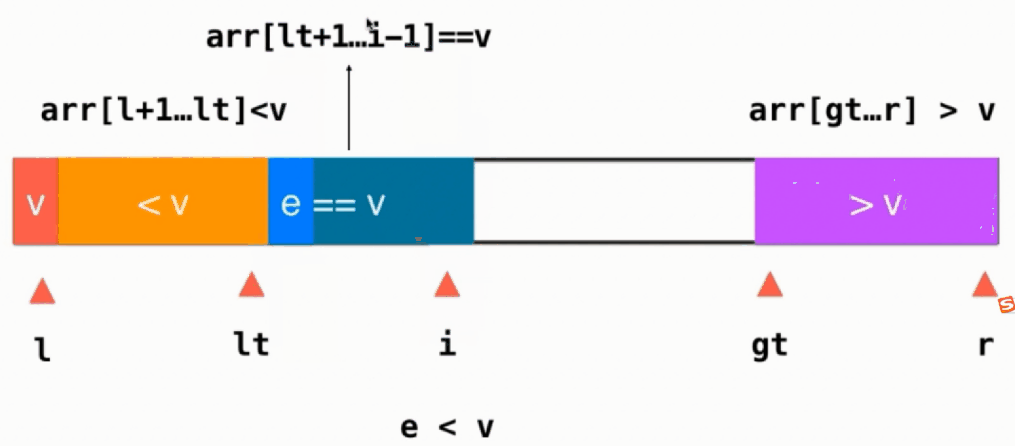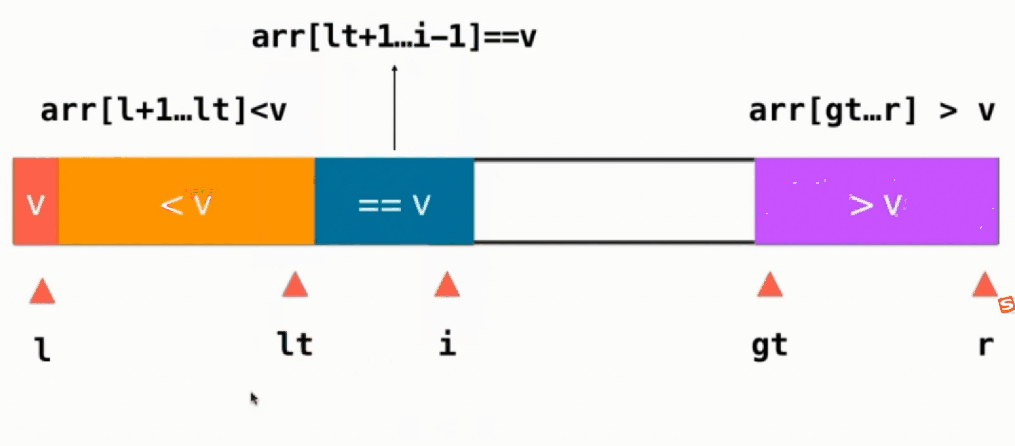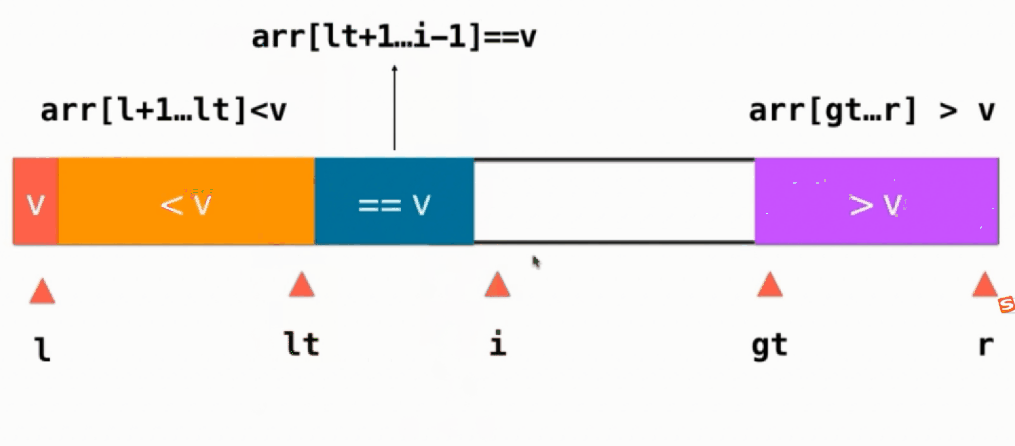
如果当前元素 e > v，则当前元素与>v部分的前面一个交换位置，即swap(arr[i], arr[gt-1])，然后gt往左移gt--,注意此时i不变，任然指向一个没有被处理的元素，只不过这个元素是从gt-1这个位置换过来的

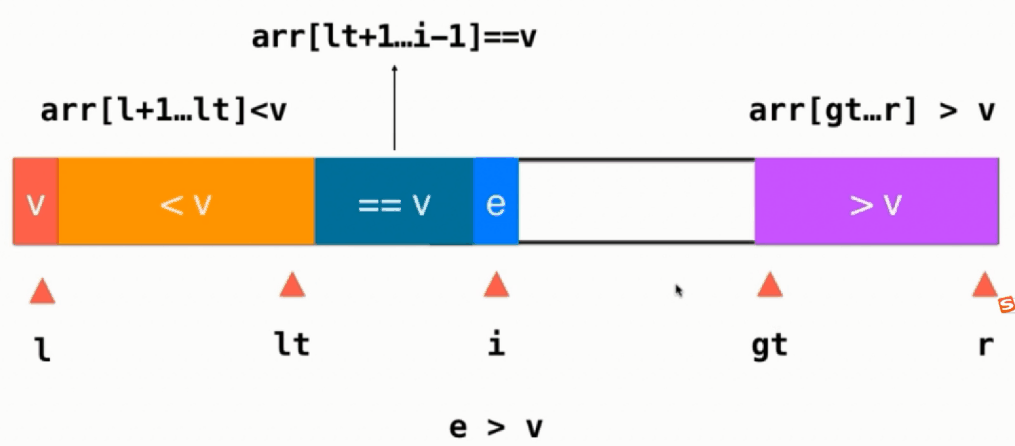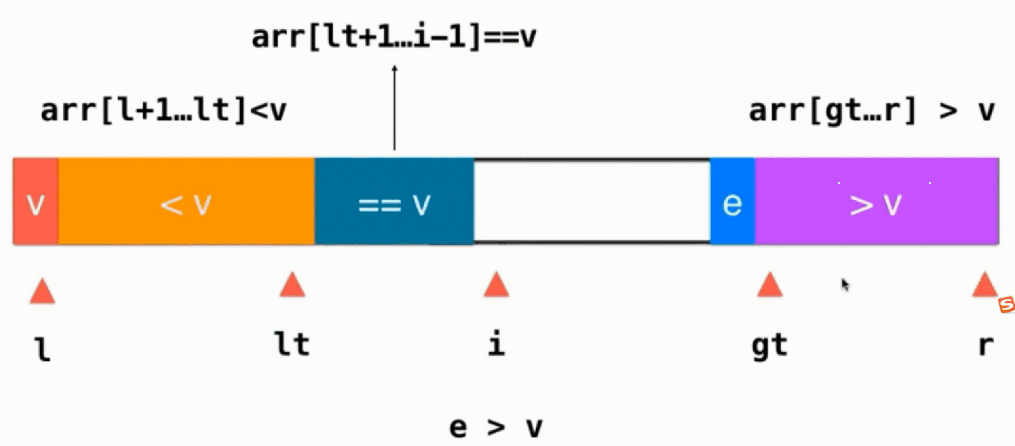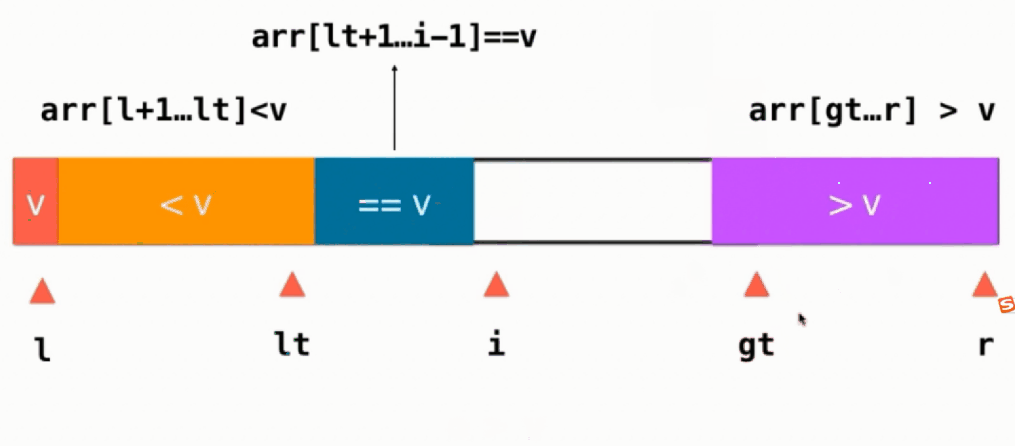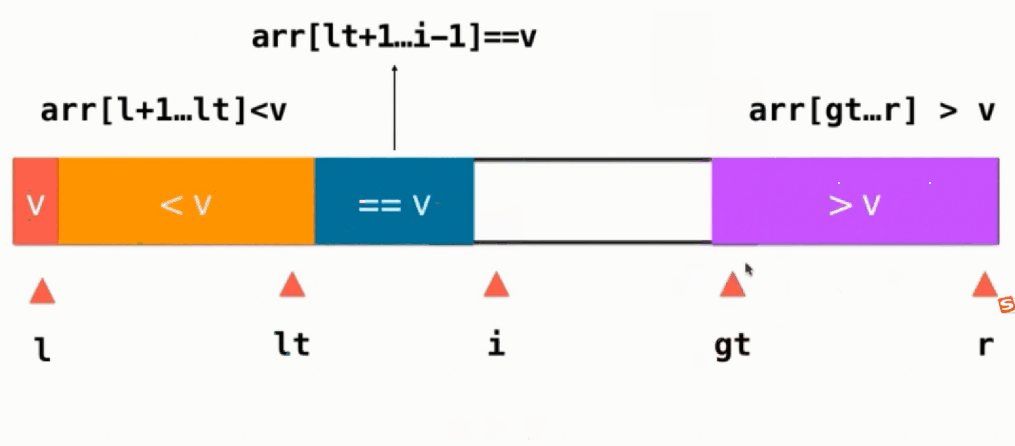
当遍历完整个序列后,即i和gt相遇,最后只需要将基准v放到排好序应该在的地方，即swap(arr[left],arr[lt])，这个时候就不用管==v的部分，只用对 <v >v的部分进行递归快速排序.

三路快速排序 代码实现

QuickSortThreeWays.c源代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include "SortHelp.h"

// arr[left+1...lt] < v  ; arr[lt+1...i-1] == v ; arr[gt...right] >v
void __QuickSortThreeWays(int *arr, int left, int right)
{
    int i, lt, gt;
    if (right - left <= 15)                     // 递归结束条件
    {
        InsertionSort(arr, left, right);
        return;
    }

    swap(&arr[left], &arr[rand() % (right - left + 1) + left]);      // 选取随机基准 与arr[left]交换
    int v = arr[left];                                               // 基准

    lt = left;           // 将初始lt代入 [left+1...lt] < v  刚好使这个区间无效
    gt = right + 1;      // 同理 gt代入  [gt...right] >v
    i = left + 1;        // 同理i代入    [lt+1...i-1] == v

    // i和gt还没遇上
    while (i < gt)
    {
        if (arr[i] < v)               // 当前元素 < 基准
        {
            swap(&arr[i], &arr[lt + 1]);
            lt++;
            i++;
        }
        else if (arr[i] > v)        // 当前元素 > 基准
        {
            swap(&arr[i], &arr[gt - 1]);
            gt--;                     // 注意i不动
        }
        else
        {                             // 等于基准
            i++;
        }
    }
    // 此时i和gt已经遇上了
    swap(&arr[left], &arr[lt--]);
    __QuickSortThreeWays(arr, left, lt);  
    __QuickSortThreeWays(arr, gt, right);
}


// 统一接口
void QuickSortThreeWays(int *arr, int n)
{
    srand(time(NULL));
    __QuickSortThreeWays(arr, 0, n - 1);
}

int main(void)
{
    // 生成随机数组测试
    int n = 1000000;
    int *arr = generateRandomArray(n, 0, n);    // 生成n个[0,n]的随机数
    testSort(arr, n, "QuickSortThreeWays", QuickSortThreeWays);

    // 生成 几乎有序的数组 最多只有2*100个元素无序
    int swapTimes = 100;
    int *arr1 = generateNearlyOrderArray(n, swapTimes);
    testSort(arr1, n, "QuickSortThreeWays", QuickSortThreeWays);

    // 生成大量重复元素数组 [0,10]
    int *arr2 = generateRandomArray(n, 0, 10);
    testSort(arr2, n, "QuickSortThreeWays", QuickSortThreeWays);

    return 0;
}

我将一路快速排序优化后，二路快速排序，三路快速排序的源代码改成.h文件,在Main.c中比较他们分别针对随机序列、几乎有序的序列、含有大量重复元素的序列分别进行效率测试，Main.c如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <stdio.h>
#include "SortHelp.h"
#include "QuickSortOneWays1.h"
#include "QuickSortTwoWays.h"
#include "QuickSortThreeWays.h"

int main(void)
{
    // 生成随机数组测试
    int n = 1000000;
    printf("\ntest generateRandomArray, size = %d, random range [0, %d]\n ", n, n);
    int *arr1 = generateRandomArray(n, 0, n);    // 生成n个[0,n]的随机数
    int *arr2 = copyArray(arr1, n);
    int *arr3 = copyArray(arr2, n);
    testSort(arr1, n, "QuickSortOneWays1", QuickSortOneWays1);
    testSort(arr2, n, "QuickSortTwoWays", QuickSortTwoWays);
    testSort(arr3, n, "QuickSortThreeWays", QuickSortThreeWays);
    free(arr1);free(arr2);free(arr3);

    // 生成 几乎有序的数组 最多只有2*100个元素无序
    int swapTimes = 100;
    printf("\ntest generateNearlyOrderArray, size = %d, sawpTimes = %d\n",n, swapTimes);
    int *arr4 = generateNearlyOrderArray(n, swapTimes);
    int *arr5 = copyArray(arr4, n);
    int *arr6 = copyArray(arr4, n);
    testSort(arr4, n, "QuickSortOneWays1", QuickSortOneWays1);
    testSort(arr5, n, "QuickSortTwoWays", QuickSortTwoWays);
    testSort(arr6, n, "QuickSortThreeWays", QuickSortThreeWays);
    free(arr4);free(arr5);free(arr6);

    // 生成大量重复元素数组 [0,10]
    printf("\ntest generateRandomArray, size = %d, random range [0, %d]\n",n, 10);
    int *arr7 = generateRandomArray(n, 0, 10);
    int *arr8 = copyArray(arr7, n);
    int *arr9 = copyArray(arr7, n);
    testSort(arr7, n, "QuickSortOneWays1", QuickSortOneWays1);
    testSort(arr8, n, "QuickSortTwoWays", QuickSortTwoWays);
    testSort(arr9, n, "QuickSortThreeWays", QuickSortThreeWays);
    free(arr7);free(arr8);free(arr9);
    return 0;
}

Clion运行结果如下：

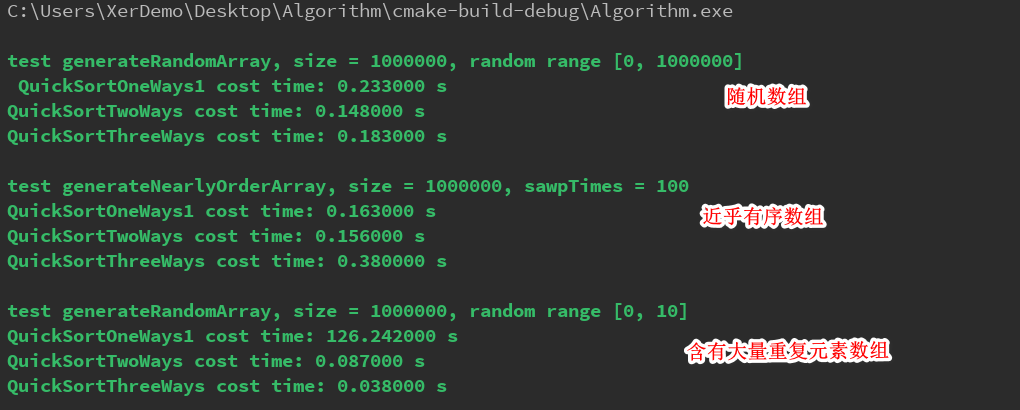
当我在把数据规模扩大10倍(把含有大量重复元素一路快排去掉)Clion运行结果如下：

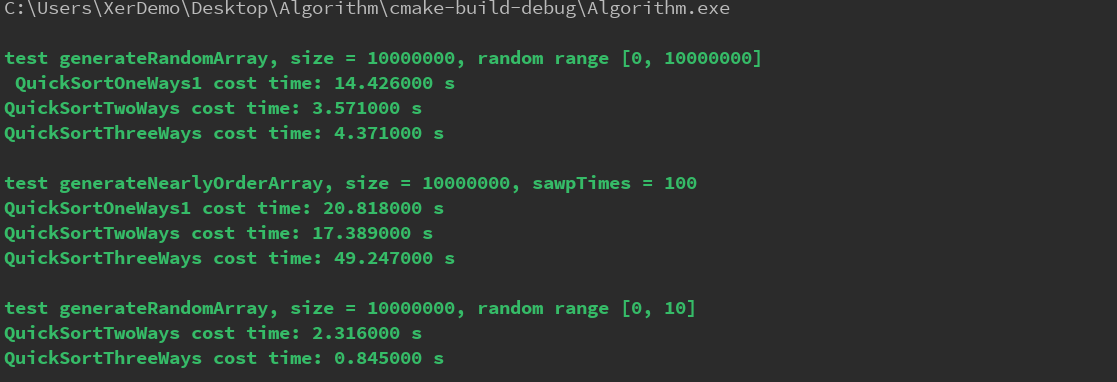
快速排序总结

总结： 当测试的规模n越大,在随机序列以及几乎有序的序列二路快速排序效率最高，在含有大量重复元素时，三路快速排序效率最高，二路快速次之，一路快速排序接近退化到O(N^2)
时间复杂度：O(Nlog2^N) 指的是平均时间复杂度
空间复杂度：O(log2^N) 递归的深度为log2^N，系统栈需要压入log2^N种状态，需要空间O(log2^N),在快排过程种定义的left,right…,都是常数级需要空间O(1),总共耗费空间O(log2^N) * O(1)。
稳定性 ：不稳定的     元素关键字相等的两个元素进行比较时会发生交换，即相对位置会发生变化
快速排序最坏的情况即基准每次是第一个元素，用因为是有序的，比基准小的元素没有，只有比基准大的元素，每次划分序列都近似于1和N-1，划分极度不均匀，像一个单链表，导致时间复杂度为O(N^2)
快速排序最好的情况下当基准能把原序列换分成均匀的两个子序列时，每一次递归层次上比较的次数都是O(N)次，而递归的深度是 log2^N (每次都是将原始序列分一半，即一直除2)，时间复杂度应为O(Nlog2^N)

pS: 相关源码链接

本文标题:快速排序实现及优化

文章作者:XerDemo

发布时间:2018-07-23, 17:54:07

最后更新:2019-08-29, 19:40:54

原始链接:https://xerdemo.github.io/2018/07/23/快速排序实现及优化/

许可协议: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

文章目录
  1. 1. Quick Sort 基本思想
  2. 2. 一路快速排序 原理演示
  3. 3. 一路快速排序 代码实现
  4. 4. 二路快速排序
  5. 5. 二路快速排序 基本思想
  6. 6. 二路快速排序 代码实现
  7. 7. 三路快速排序
  8. 8. 三路快速排序 代码实现
  9. 9. 快速排序总结
|