归并排序(自顶向下，自底向上)

Algorithm


本文将介绍从归并排序

归并排序基本思想

基本思想:将大小为N的序列看成N个长度为1的子序列，接下来将相邻的子序列两两进行归并操作，形成N/2(+1)个长度为2(或1)的有序子序列；然后再继续进行相邻子序列两两归并操作，如此一直循环，直到剩下1个长度为N的序列，则待序列为原序列完成排序后的结果。动画演示如下：

原理

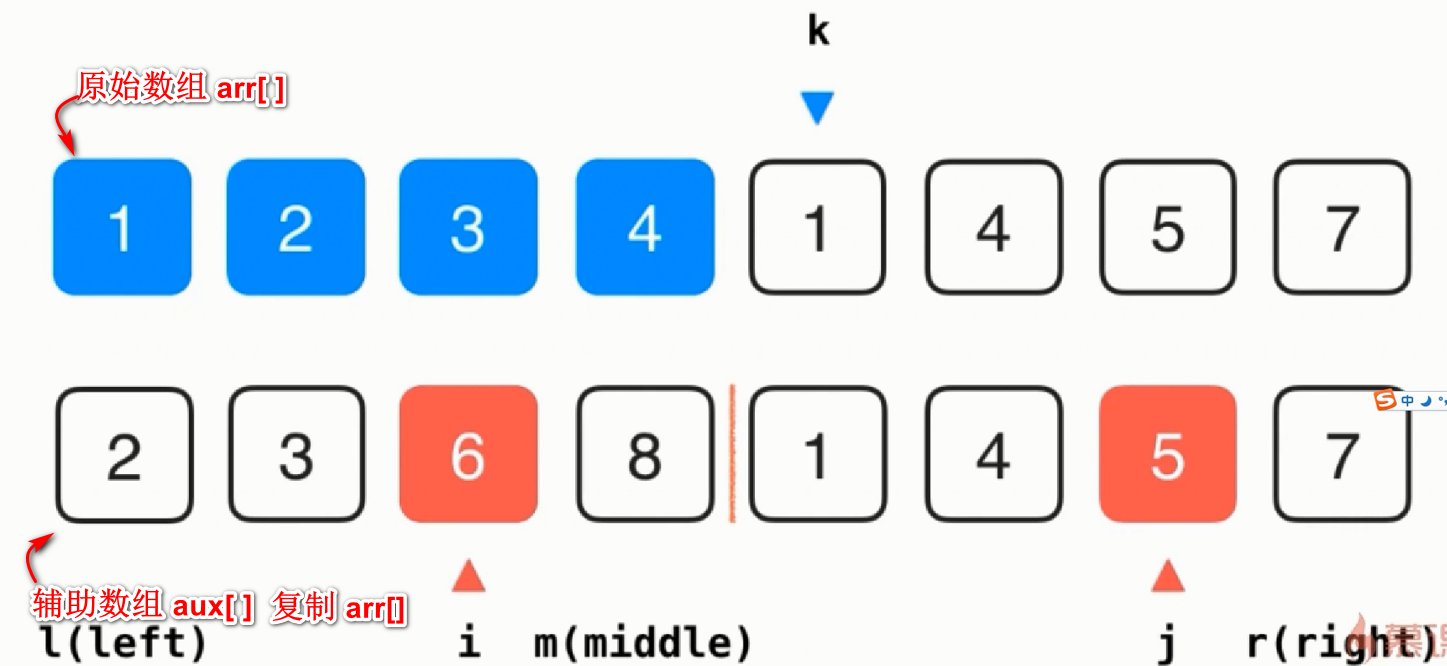
其中归并的过程具体如下，选取2 3 6 8 1 4 5 7这个即将要归并成一个序列的归并过程来讲归并的实现。动画演示如下：

原理

解释上面的动画过程，用一个辅助数组aux[]复制即将整合的两个序列，初始时 i指向第一个序列的起始位置，j指向第二个序列的起始位置。当aux[i-left] < aux[j-left]要减去left的偏移量，则arr[k]= arr[i-left]，k++, i++,j不变;如果aux[i-left] >= aux[j-left]，则arr[k]= arr[j-left]，k++, j++,i不变;如果第一个序列结束 将第二个序列搬到arr[];如果如果第二个序列结束 将第一个序列搬到arr[]

原理

自顶向下归并排序源代码

SortHelper.h 存放归并排序需要的相关函数:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
#ifndef ALGORITHM_SORTHELPER_H
#define ALGORITHM_SORTHELPER_H
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

// 生成有n个元素的随机数组,每个元素的随机范围为[rangeL, rangeR]
int *generateRandomArray(int n, int rangeL, int rangeR)
{
    int * arr = NULL;
    int i;
    if (n > 0 && rangeL <= rangeR)
    {
        arr = (int *) malloc(sizeof(int) * n);          // 用malloc 分配数组 是因为不用malloc的话 随着此函数的结束 数组空间会被释放掉
        srand(time(NULL));
        for (i = 0; i < n; ++i)
        {
            arr[i] = rand() % (rangeR - rangeL + 1) + rangeL;  // 注意区间是[rangeL, rangeR]
        }
    }
    return arr;
}

// 交换两个数位置
void swap(int *a, int *b)
{
    int temp = *a;
    *a = *b;
    *b = temp;
}

// 生成近乎有序的数组  n数据个数  swapTimes:交换次数  最多只有2*交换次数个元素无序
int * generateNearlyOrderArray(int n, int swapTimes)
{
    int i;
    int *arr = NULL;
    if (n > 0)
    {
        arr = (int *) malloc(sizeof(int) * n);
        for (i = 0; i < n; ++i)
        {
            arr[i] = i;
        }

        srand(time(NULL));
        for (i = 0; i < swapTimes; ++i)
        {
            int x = rand() % n;
            int y = rand() % n;
            swap(&arr[x], &arr[y]);
        }
    }
    return arr;
}

// 插入排序
void InsertionSort(int * arr, int left, int right)
{
    int i, j;
    for (i = left + 1; i <= right; ++i)
    {
        int temp = arr[i];
        for (j = i; j > left && arr[j-1] > temp; j--)
        {
            arr[j] = arr[j - 1];
        }
        arr[j] = temp;
    }
}

// 打印数组
void printArray(int *arr, int n)
{
    int i;
    for (i = 0; i < n; ++i)
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}


void testSort(char * sortName, void(*sort)(int* , int ), int * arr, int n)
{
    clock_t startTime = clock();
    sort(arr, n);
    clock_t endTime = clock();
    printf("%s cost: %lfs\n",sortName, (double)(endTime - startTime) / CLOCKS_PER_SEC);
}

// 拷贝arr数组
int * copyArray(int *arr, int n)
{
    int i;
    int *arr2 = (int *) malloc(sizeof(int) * n);
    for (i = 0; i < n; ++i)
    {
        arr2[i] = arr[i];
    }
    return arr2;
}
#endif //ALGORITHM_SORTHELPER_H

MergeSort1.c自顶向下源码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "SortHelper.h"

// 将arr[left ... right] 进行归并操作
void __merge1(int *arr, int left, int mid, int right)
{
    int i, j, k;
    int aux[right - left + 1];              // 辅助数组aux[]  复制即将整合的两个序列
    for (i = left; i <= right; ++i)
    {
        aux[i - left] = arr[i];             // aux[] 复制 arr[]的内容
    }

    i = left, j = mid + 1;                  // i指向第一个序列的起始位置  j指向第二个序列的起始位置

    for (k = left; k <= right; ++k)
    {
        if (i > mid)                        // 如果第一个序列结束  将第二个序列搬到arr[]
        {
            arr[k] = aux[j - left];
            j++;
        }
        else if (j > right)                 // 如果第二个序列结束  将第一个序列搬到arr[]
        {
            arr[k] = aux[i-left];
            i++;
        }
        else if (aux[i-left] < aux[j-left])  // 如果此时i指向的元素 小于 j
        {
            arr[k] = aux[i - left];
            i++;
        }
        else{
            arr[k] = aux[j - left];
            j++;
        }
    }
}

// 对arr[left ... right] 进行归并排序
void __mergeSort1(int *arr, int left, int right)
{
    if (left >= right)
    {
        return;
    }
    int mid = left + (right - left) / 2;
    __mergeSort1(arr, left, mid);           // 对左子序列进行归并排序
    __mergeSort1(arr, mid + 1, right);      // 对右子序列进行归并排序
    __merge1(arr, left, mid , right);       // 将左子序列 右子序列进行归并操作
}

void mergeSort1(int *arr, int n)
{
    __mergeSort1(arr, 0, n - 1);
}

int main(void)
{
    int n = pow(10, 7);
    // 测试随机数组
    int *arr = generateRandomArray(n, 0, n);
    testSort("mergeSort1", mergeSort1, arr, n);
    free(arr);

    // 测试几乎有序的数组
    int swapTimes = 100;
    int *arr1 = generateNearlyOrderArray(n, swapTimes);
    testSort("mergeSort1", mergeSort1, arr1, n);
    free(arr1);

    // 测试含有大量重复元素的数组  n个数组 范围[0,10]
    int *arr2 = generateRandomArray(n, 0, 10);
    testSort("mergeSort1", mergeSort1, arr2, n);
    free(arr2);
    return 0;
}

自顶向下归并排序Clion运行结果：(数据规模10000000 1千万)

原理

还有两个地方可以优化：

  • 对于小规模数组,使用插入排序
  • 对于arr[mid] <= arr[mid+1]的情况 不进行merge 因为已经有序

优化后自顶向下的归并排序 MergeSort2.c

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include "SortHelper.h"

// 将arr[left ... right] 进行归并操作
void __merge2(int *arr, int left, int mid, int right)
{
    int i, j, k;
    int aux[right - left + 1];              // 辅助数组aux[]  复制即将整合的两个序列
    for (i = left; i <= right; ++i)
    {
        aux[i - left] = arr[i];             // aux[] 复制 arr[]的内容
    }

    i = left, j = mid + 1;                  // i指向第一个序列的起始位置  j指向第二个序列的起始位置

    for (k = left; k <= right; ++k)
    {
        if (i > mid)                        // 如果第一个序列结束  将第二个序列搬到arr[]
        {
            arr[k] = aux[j - left];
            j++;
        }
        else if (j > right)                 // 如果第二个序列结束  将第一个序列搬到arr[]
        {
            arr[k] = aux[i-left];
            i++;
        }
        else if (aux[i-left] < aux[j-left])  // 如果此时i指向的元素 小于 j
        {
            arr[k] = aux[i - left];
            i++;
        }
        else{
            arr[k] = aux[j - left];
            j++;
        }
    }
}

// 在__mergeSort1的基础上两个地方进行优化
// 对arr[left ... right] 进行归并排序
void __mergeSort2(int *arr, int left, int right)
{
    // 优化1： 对于小规模数组,使用插入排序
    if (right - left <= 15)
    {
        InsertionSort(arr, left, right);
        return;
    }
    int mid = left + (right - left) / 2;
    __mergeSort2(arr, left, mid);
    __mergeSort2(arr, mid + 1, right);
    // 优化2： 对于arr[mid] <= arr[mid+1]的情况 不进行merge 因为已经有序
    // 对于近乎有序的数组非常有效 但是对于一般情况，有一定的性能损失（判读需要时间）
    if (arr[mid] > arr[mid + 1])
    {
        __merge2(arr, left, mid , right);
    }

}

void mergeSort2(int *arr, int n)
{
    __mergeSort2(arr, 0, n - 1);
}

int main(void)
{
    int n = pow(10, 7);
    // 测试随机数组
    int *arr = generateRandomArray(n, 0, n);
    testSort("mergeSort2", mergeSort2, arr, n);
    free(arr);

    // 测试几乎有序的数组
    int swapTimes = 100;
    int *arr1 = generateNearlyOrderArray(n, swapTimes);
    testSort("mergeSort2", mergeSort2, arr1, n);
    free(arr1);

    // 测试含有大量重复元素的数组  n个数组 范围[0,10]
    int *arr2 = generateRandomArray(n, 0, 10);
    testSort("mergeSort2", mergeSort2, arr2, n);
    free(arr2);
    return 0;
}

自顶向下归并排序(优化后)Clion运行结果：(数据规模10000000 1千万)

原理

自底向上的归并排序

自底向上的归并排序MergeSortBU.c如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <stdio.h>
#include "MergeSort1.h"
#include "SortHelper.h"

int min(int a, int b)
{
    return a > b ? b : a;
}

void mergeSortBU(int *arr, int n)
{
    int size, i;
    for (size = 1; size <= n; size += size)             // 规模 每次扩大两倍
    {
        for (i = 0; i + size < n; i += 2 * size)
        {
            // 对 arr[i...i+size-1] 和 arr[i+size...i+2*size-1] 进行归并
            // 循环条件i+size < n 是为了确保第二部分的存在 也保证了i+size-1(第一个子序列)不会越界
            // 为了确保第二个子序列不会越界 min(i + 2 * size - 1, n-1)
            __merge1(arr, i, i + size - 1, min(i + 2 * size - 1, n - 1));
        }
    }
}

// 在mergeSortBU的基础上两个地方进行优化
void mergeSortBU2(int *arr, int n)
{
    int size, i;
    // 优化1： 对于小规模数组,使用插入排序
    for (i = 0; i < n; i += 16)
    {
        InsertionSort(arr, i, min(i + 15, n - 1));
    }

    for (size = 16; size <= n; size += size)             // 规模 每次扩大两倍
    {
        for (i = 0; i + size < n; i += 2 * size)
        {
            // 优化2： 对于arr[i + size - 1] > arr[i + size]的情况 不进行merge 因为已经有序
            if (arr[i + size - 1] > arr[i + size])
            {
                __merge1(arr, i, i + size - 1, min(i + 2 * size - 1, n - 1));
            }
        }
    }
}

int main(void)
{
    int n = pow(10, 7);
    // 测试随机数组
    int *arr = generateRandomArray(n, 0, n);
    int *arr1 = copyArray(arr, n);
    testSort("mergeSortBU", mergeSortBU, arr, n);
    testSort("mergeSortBU2", mergeSortBU2, arr1, n);
    free(arr);
    free(arr1);

    // 测试几乎有序的数组
    int swapTimes = 100;
    int *arr2 = generateNearlyOrderArray(n, swapTimes);
    int *arr3 = copyArray(arr2, n);
    testSort("mergeSortBU", mergeSortBU, arr2, n);
    testSort("mergeSortBU2", mergeSortBU2, arr3, n);
    free(arr2);
    free(arr3);

    // 测试含有大量重复元素的数组  n个数组 范围[0,10]
    int *arr4 = generateRandomArray(n, 0, 10);
    int *arr5 = copyArray(arr4, n);
    testSort("mergeSortBU", mergeSortBU, arr4, n);
    testSort("mergeSortBU2", mergeSortBU2, arr5, n);
    free(arr4);
    free(arr5);
    return 0;
}

自底向上归并排序Clion运行结果：(数据规模10000000 1千万)

原理

总结

将MergeSort1.c,MergeSort2.c,MergeSortBU.c更改为.h,新建Main.c如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <stdio.h>
#include "SortHelper.h"
#include "MergeSort2.h"
#include "MergeSortBU.h"

int main(void)
{
    int n = pow(10, 8);
    // 测试随机数组
    printf("test generateRandomArray, size = %d, random range [0, %d]\n", n, n);
    int *arr = generateRandomArray(n, 0, n);
    int *arr1 = copyArray(arr, n);
    int *arr2 = copyArray(arr, n);
    int *arr3 = copyArray(arr, n);
    testSort("mergeSort1", mergeSort1, arr, n);
    testSort("mergeSort2", mergeSort2, arr1, n);
    testSort("mergeSortBU", mergeSortBU, arr2, n);
    testSort("mergeSortBU2", mergeSortBU2, arr3, n);
    free(arr);free(arr1);free(arr2);free(arr3);

    // 测试几乎有序的数组
    int swapTimes = 100;
    printf("\ntest generateNearlyOrderArray, size = %d, sawpTimes = %d\n",n, swapTimes);
    int *arr4 = generateNearlyOrderArray(n, swapTimes);
    int *arr5 = copyArray(arr4, n);
    int *arr6 = copyArray(arr4, n);
    int *arr7 = copyArray(arr4, n);
    testSort("mergeSort1", mergeSort1, arr4, n);
    testSort("mergeSort2", mergeSort2, arr5, n);
    testSort("mergeSortBU", mergeSortBU, arr6, n);
    testSort("mergeSortBU2", mergeSortBU2, arr7, n);
    free(arr4);free(arr5);free(arr6);free(arr7);

    // 测试含有大量重复元素的数组  n个数组 范围[0,10]
    printf("\ntest generateRandomArray, size = %d, random range [0, %d]\n",n, 10);
    int *arr8 = generateRandomArray(n, 0, 10);
    int *arr9 = copyArray(arr8, n);
    int *arr10 = copyArray(arr8, n);
    int *arr11 = copyArray(arr8, n);
    testSort("mergeSort1", mergeSort1, arr8, n);
    testSort("mergeSort2", mergeSort2, arr9, n);
    testSort("mergeSortBU", mergeSortBU, arr10, n);
    testSort("mergeSortBU2", mergeSortBU2, arr11, n);
    free(arr8);free(arr9);free(arr10);free(arr11);
    return 0;
}

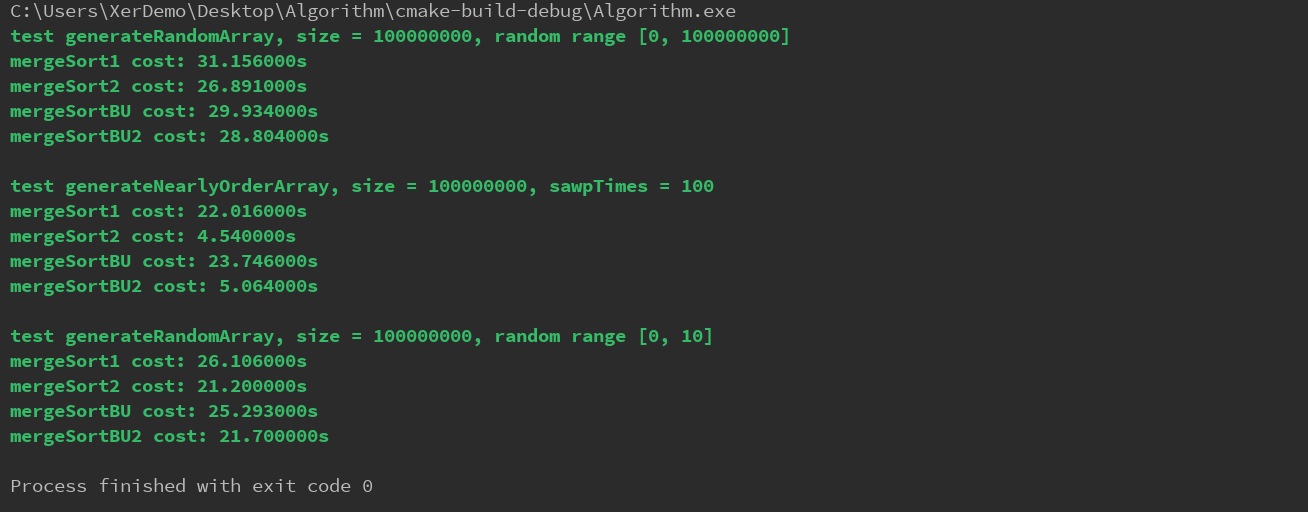
Clion运行结果如下,规模又扩大了10倍(1亿)

原理

相关源代码下载链接

本文标题:归并排序(自顶向下，自底向上)

文章作者:XerDemo

发布时间:2018-07-28, 15:24:44

最后更新:2019-06-15, 21:29:44

原始链接:https://xerdemo.github.io/2018/07/28/归并排序/

许可协议: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

文章目录
  1. 1. 归并排序基本思想
  2. 2. 自顶向下归并排序源代码
  3. 3. 自底向上的归并排序
  4. 4. 总结
|