插入排序基本思想
基本思想:待排序的一组序列分为已经排好序的和未排好序的两个部分;初始状态时,已排序的序列仅包含第一个元素,未排序的序列中元素未除去第一个以外N-1个元素;此后将未排序的元素依次插入到已排序的序列中。如此往复,经过N-1次插入后,未排序序列中元素个数为0,则排序完成。
可以把插入排序想象成打扑克时,拿牌的过程,首先右手先拿一张牌,放入左手此时只有一张牌且已经有序,右再拿一张牌,与当前已经有序的牌从右到左进行比较,放到适合的位置,重复此过程直到排序完成。
具体实现:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后
- 重复步骤2~5
动画演示:

插入排序代码
SortHelper.h存放相关工具函数1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
// 生成有n个元素的随机数组,每个元素的随机范围为[rangeL, rangeR]
int *generateRandomArray(int n, int rangeL, int rangeR)
{
int * arr = NULL;
int i;
if (n > 0 && rangeL <= rangeR)
{
arr = (int *) malloc(sizeof(int) * n); // 用malloc 分配数组 是因为不用malloc的话 随着此函数的结束 数组空间会被释放掉
srand(time(NULL));
for (i = 0; i < n; ++i)
{
arr[i] = rand() % (rangeR - rangeL + 1) + rangeL; // 注意区间是[rangeL, rangeR]
}
}
return arr;
}
// 交换两个数位置
void swap(int *a, int *b)
{
int temp = *a;
*a = *b;
*b = temp;
}
// 生成近乎有序的数组 n数据个数 swapTimes:交换次数 最多只有2*交换次数个元素无序
int * generateNearlyOrderArray(int n, int swapTimes)
{
int i;
int *arr = NULL;
if (n > 0)
{
arr = (int *) malloc(sizeof(int) * n);
for (i = 0; i < n; ++i)
{
arr[i] = i;
}
srand(time(NULL));
for (i = 0; i < swapTimes; ++i)
{
int x = rand() % n;
int y = rand() % n;
swap(&arr[x], &arr[y]);
}
}
return arr;
}
// 生成近乎倒序的数组 n数据个数 swapTimes:交换次数 最多只有2*交换次数个元素无序 左闭右开
int * generateNearlyReverseOrderArray(int n, int swapTimes)
{
int i;
int *arr = NULL;
if (n > 0)
{
arr = (int *) malloc(sizeof(int) * n);
for (i = 0; i < n; ++i)
{
arr[i] = n-1-i;
}
srand(time(NULL));
for (i = 0; i < swapTimes; ++i)
{
int x = rand() % n;
int y = rand() % n;
swap(&arr[x], &arr[y]);
}
}
return arr;
}
// 插入排序
void InsertionSort(int * arr, int left, int right)
{
int i, j;
for (i = left + 1; i <= right; ++i)
{
int temp = arr[i];
for (j = i; j > left && arr[j-1] > temp; j--)
{
arr[j] = arr[j - 1];
}
arr[j] = temp;
}
}
// 打印数组
void printArray(int *arr, int n)
{
int i;
for (i = 0; i < n; ++i)
{
printf("%d ", arr[i]);
}
printf("\n");
}
void testSort(char * sortName, void(*sort)(int* , int ), int * arr, int n)
{
clock_t startTime = clock();
sort(arr, n);
clock_t endTime = clock();
printf("%s cost: %lfs\n",sortName, (double)(endTime - startTime) / CLOCKS_PER_SEC);
}
// 拷贝arr数组
int * copyArray(int *arr, int n)
{
int i;
int *arr2 = (int *) malloc(sizeof(int) * n);
for (i = 0; i < n; ++i)
{
arr2[i] = arr[i];
}
return arr2;
}
InsertionSort.c插入排序源码如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
void insertionSort1(int *arr, int n)
{
int i, j;
for (i = 1; i < n; ++i)
{
// for (j = i; j>0; --j)
// {
// if (arr[j] < arr[j - 1])
// {
// swap(&arr[j], &arr[j - 1]);
// }
// else
// {
// break;
// }
// }
// 可以改写成这样 注意i从1开始 j是>0
for (j = i; j > 0 && arr[j] < arr[j - 1]; --j)
{
swap(&arr[j], &arr[j - 1]);
}
}
}
// 优化的插入排序 将交换(每次做三步赋值) 换成了 赋值
void insertionSort2(int *arr, int n)
{
int i, j;
for (i = 1; i < n; ++i)
{
int temp = arr[i]; // 取出未排序序列中的第一个元素
// 在已排序元素中 从后往前扫描 如果发现比temp大 则往后移一位
for (j = i; j > 0 && arr[j-1] > temp; --j)
{
arr[j] = arr[j-1];
}
arr[j] = temp; // temp进入适合的位置
}
}
int main(void)
{
int n = 100000;
// 随机数组 区间[0,n]
printf("test RandomArray size = %d [0,%d]\n", n, n);
int *arr = generateRandomArray(n, 0, n);
int *arr1 = copyArray(arr, n);
testSort("insertionSort1", insertionSort1, arr, n);
testSort("insertionSort2 ", insertionSort2, arr1, n);
// 近乎有序的数组 swapTimes:交换次数 区间[0,n)
int swapTimes = 100;
printf("\ntest NearlyOrderArray size = %d [0,%d) swapTimes: %d\n", n, n, swapTimes);
int *arr2 = generateNearlyOrderArray(n, swapTimes);
int *arr3 = copyArray(arr, n);
testSort("insertionSort1 ", insertionSort1, arr2, n);
testSort("insertionSort2", insertionSort2, arr3, n);
// 近乎倒序的数组 区间[0,n)
printf("\ntest NearlyReverseArray size = %d [0,%d) swapTimes: %d\n", n, n, swapTimes);
int *arr4 = generateNearlyReverseOrderArray(n, swapTimes);
int *arr5 = copyArray(arr4, n);
testSort("insertionSort1 ", insertionSort1, arr4, n);
testSort("insertionSort2 ", insertionSort2, arr5, n);
// 含大量重复元素的数组 [0,10]
printf("\ntest RandomArray size = %d [0,10]\n", n);
int *arr6 = generateRandomArray(n, 0, 10);
int *arr7 = copyArray(arr6, n);
testSort("insertionSort1 ", insertionSort1, arr6, n);
testSort("insertionSort2", insertionSort2, arr7, n);
free(arr);free(arr1);free(arr2);free(arr3);free(arr4);free(arr5);free(arr6);free(arr7);
return 0;
}
Clion运行结果如下:
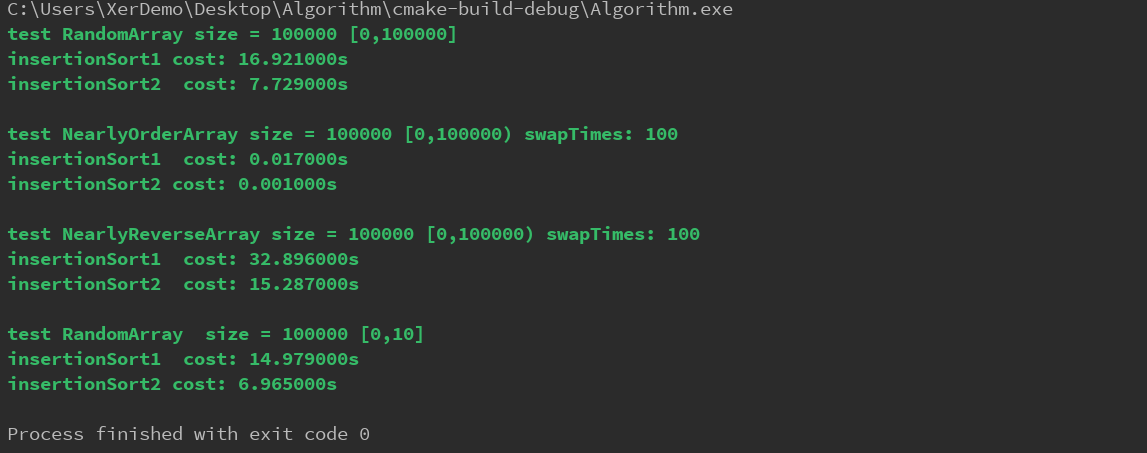
总结
时间复杂度:O(n^2) 指的是平均时间复杂度空间复杂度:O(1) 拿insertionSort2来说 只开辟了i,j,temp等常数个空间
稳定性 : 稳定的 元素关键字相等的两个元素进行比较时并不会发生交换,即相对位置不会发生变化
插入排序最坏的情况下对应的每一个i,要进行i-1次比较和交换,时间复杂度O(N^2)
插入排序最好的情况下(序列已经有序),只用执行第一层循环就行了O(N)
pS:源代码链接