队列
栈的特点:先进先出 First In First Out(FIFO)
一种操作受限的线性表,只允许在队头删除元素,队尾插入元素
相比于数组,队列对应的操作是数组的子集
顺序队列
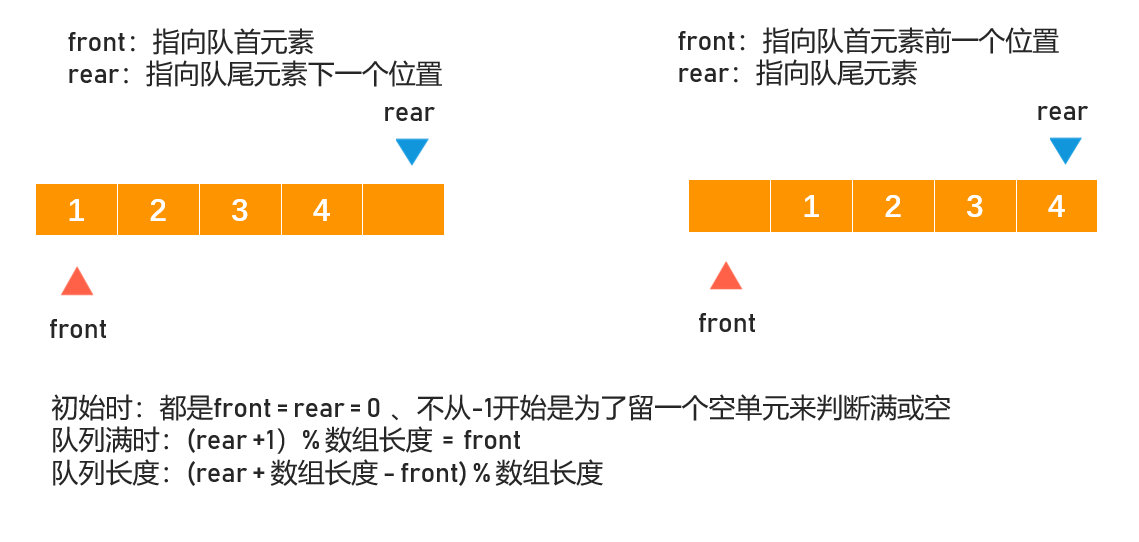
基本思想:分配一块连续的存储单元存放队列中的元素,并设下头指针front:指向队首元素,尾指针rear:指向队尾元素的后一个元素
也可以front指向队首元素的前一个元素,rear指向队尾元素,但是在进行操作时需要相应的变化
节点定义:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| #define INITSIZE 5
#define E int
typedef struct {
E *data;
int capacity;
int front;
int rear;
} SeqQueue;
|
初始化及一些其他操作:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
SeqQueue *initQueue() {
SeqQueue *queue = (SeqQueue *) malloc(sizeof(SeqQueue));
queue->data = (E *) malloc(sizeof(E) * INITSIZE);
queue->capacity = INITSIZE;
queue->front = queue->rear = 0;
}
int getCapacity(SeqQueue *queue) {
return queue->capacity;
}
int isEmpty(SeqQueue *queue) {
return queue->front == queue->rear;
}
int getSize(SeqQueue *queue) {
return queue->rear - queue->front;
}
void printMessage(SeqQueue *queue) {
printf("Queue:size = %d , capacity = %d \n", getSize(queue), getCapacity(queue));
if (isEmpty(queue)) {
printf("printMessage failed. Queue is empty.\n");
return;
}
int i;
printf("front [");
for (i = queue->front; i < queue->rear; ++i) {
printf("%d", queue->data[i]);
if (i != queue->rear - 1) {
printf(", ");
}
}
printf("] rear\n");
}
|
入队: 如果队列满则动态增长数组空间(队满:rear == capacity)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
void resize(SeqQueue *queue, int newCapacity) {
E *newDate = (E *) malloc(sizeof(E) * newCapacity);
int i,j = queue->front;
for (i = 0; i < getSize(queue); ++i) {
newDate[i] = queue->data[j++];
}
queue->data = newDate;
queue->rear = getSize(queue);
queue->front = 0;
queue->capacity = newCapacity;
}
void enqueue(SeqQueue *queue, E e) {
if (queue->rear == queue->capacity) {
resize(queue, 2 * queue->capacity);
}
queue->data[queue->rear] = e;
queue->rear++;
}
|
出队: 如果队列空则不能出队
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
|
E dequeue(SeqQueue *queue) {
if (isEmpty(queue)) {
printf("dequeue failed. Queue is empty.\n");
return -9999999;
}
E res = queue->data[queue->front];
queue->front++;
if (getSize(queue) == queue->capacity / 2) {
resize(queue, queue->capacity / 2);
}
return res;
}
|
读取队头元素:
1
2
3
4
5
6
7
8
|
E getFront(SeqQueue *queue) {
if (isEmpty(queue)) {
printf("getFront failed. Queue is empty.\n");
return -9999999;
}
return queue->data[queue->front];
}
|
顺序队列的缺点:队尾溢出,但是实际上数组仍有空间,从而引出了循环队列
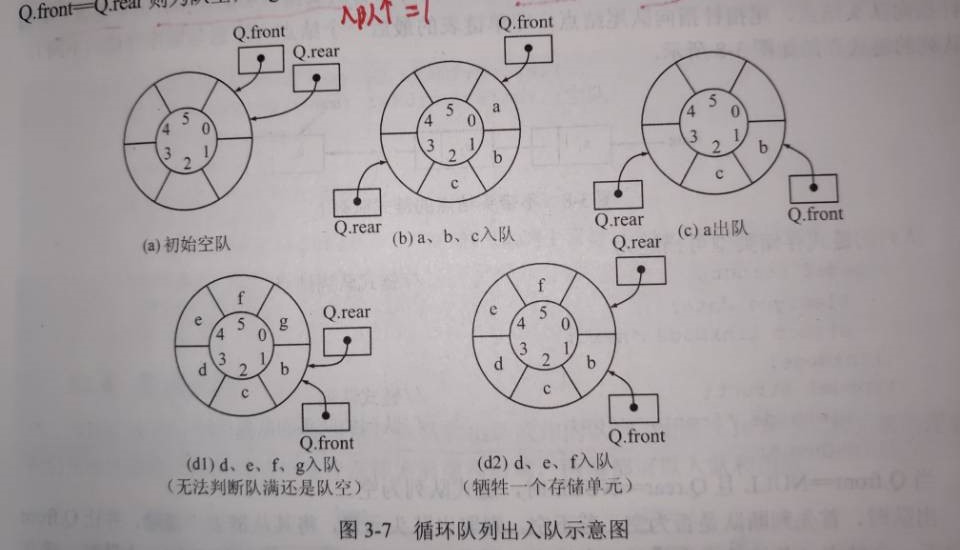
循环队列
为了解决队尾溢出而实际上数组仍然有空余空间的问题,一般在队列的顺序存储结构中采用循环队列的方式:rear和front到达数组端点时,能折回到数组开始处,即相当于将数组头尾相接,想象成环状,如图所示。当插人和删除操作的作用单元达到数组的末端后,用公式“Rear(或Front)%数组长度”取余运算就可以实现折返到起始单元
判断队满还是对空的3种方法:
- 牺牲一个单元来区分队空和队满,入队时少用一个队列单元(上图的d2)
选用
- 类型中增设表示元素个数的数据成员.对空为size==0,队满为size==MAXSIZE,这两种情况都有front == rear
- 类型中增设tag成员,出队是tag==0,若因出队导致则为队空;入队时tag == 1,若因入队导致,则为队满
节点定义和相关操作
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| #define INITSIZE 5
#define E int
typedef struct {
E *data;
int capacity;
int front;
int rear;
} LoopQueue;
LoopQueue *initQueue() {
LoopQueue *queue = (LoopQueue *) malloc(sizeof(LoopQueue));
queue->data = (E *) malloc(sizeof(E) * INITSIZE);
queue->capacity = INITSIZE;
queue->front = queue->rear = 0;
}
int getCapacity(LoopQueue *queue) {
return queue->capacity - 1;
}
int isEmpty(LoopQueue *queue) {
return queue->front == queue->rear;
}
int getSize(LoopQueue *queue) {
return (queue->rear + queue->capacity - queue->front) % queue->capacity;
}
void printMessage(LoopQueue *queue) {
printf("Queue:size = %d , capacity = %d \n", getSize(queue), getCapacity(queue));
if (isEmpty(queue)) {
printf("printMessage failed. Queue is empty.\n");
return;
}
int i;
printf("%d %d\n", queue->front, queue->rear);
printf("front [");
for (i = queue->front; i < queue->rear; ++i) {
printf("%d", queue->data[i]);
if (i != queue->rear - 1) {
printf(", ");
}
}
printf("] rear\n");
}
|
入队:先判断是否满
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
|
void resize(LoopQueue *queue, int newCapacity) {
E *newDate = (E *) malloc(sizeof(E) * newCapacity + 1);
int i;
for (i = 0; i < getSize(queue); ++i) {
newDate[i] = queue->data[(i + queue->front) % queue->capacity];
}
queue->data = newDate;
queue->rear = getSize(queue);
queue->front = 0;
queue->capacity = newCapacity + 1;
}
void enqueue(LoopQueue *queue, E e) {
if ((queue->rear + 1) % queue->capacity == queue->front) {
resize(queue, 2 * queue->capacity);
}
queue->data[queue->rear] = e;
queue->rear = (queue->rear + 1) % queue->capacity;
}
|
出队:先判断是否空
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
E dequeue(LoopQueue *queue) {
if (isEmpty(queue)) {
printf("dequeue failed. Queue is empty.\n");
return -9999999;
}
E res = queue->data[queue->front];
queue->front = (queue->front + 1) % queue->capacity;
if (getSize(queue) == queue->capacity / 2) {
resize(queue, queue->capacity / 2);
}
return res;
}
|
获取队头元素:
1
2
3
4
5
6
7
8
|
E getFront(LoopQueue *queue) {
if (isEmpty(queue)) {
printf("getFront failed. Queue is empty.\n");
return -9999999;
}
return queue->data[queue->front];
}
|
ps: 只能使用数组长度-1个空间
链式队列
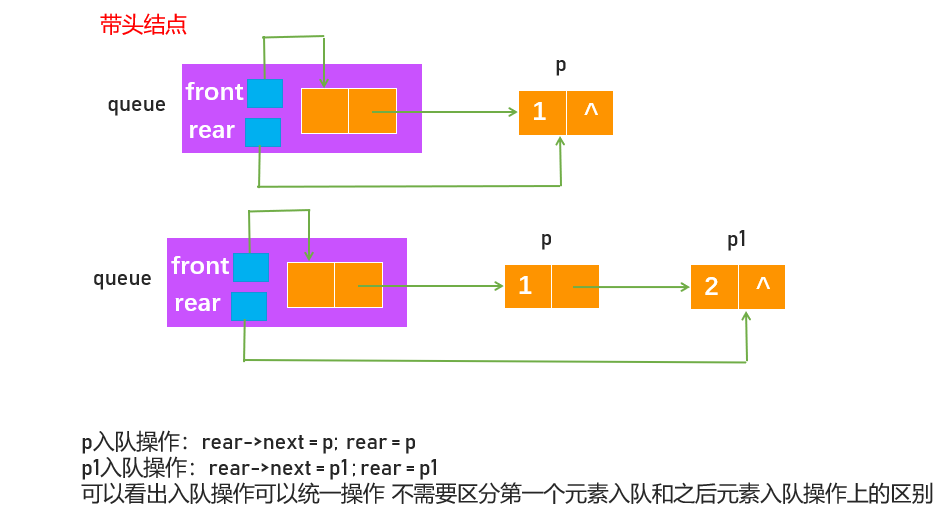
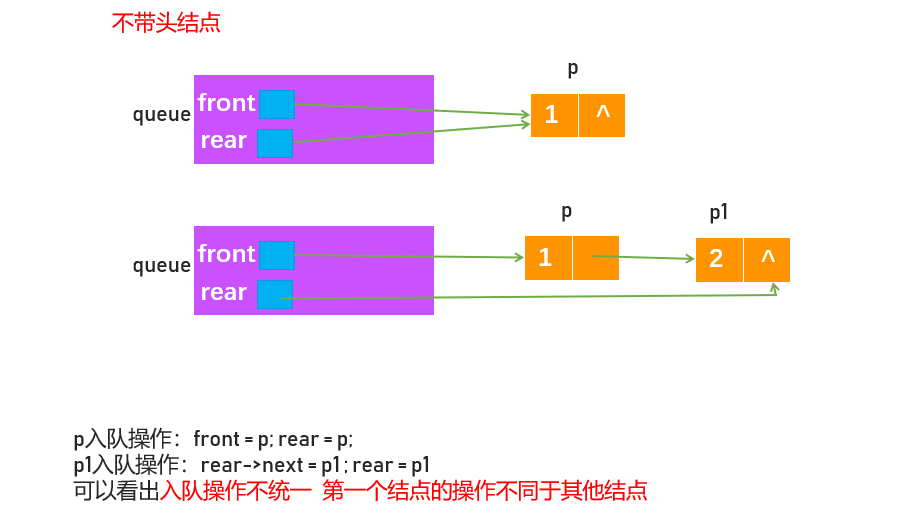
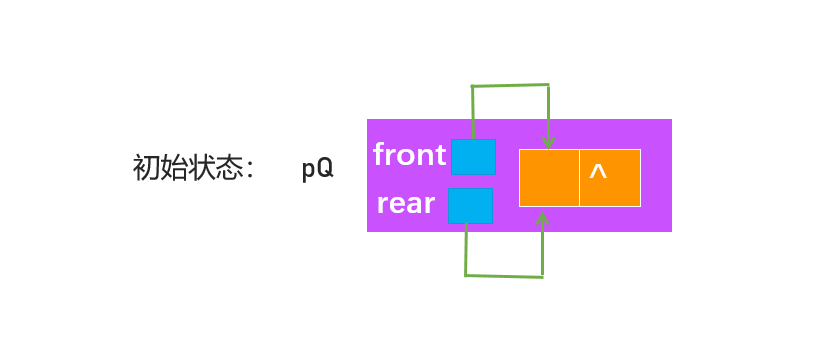
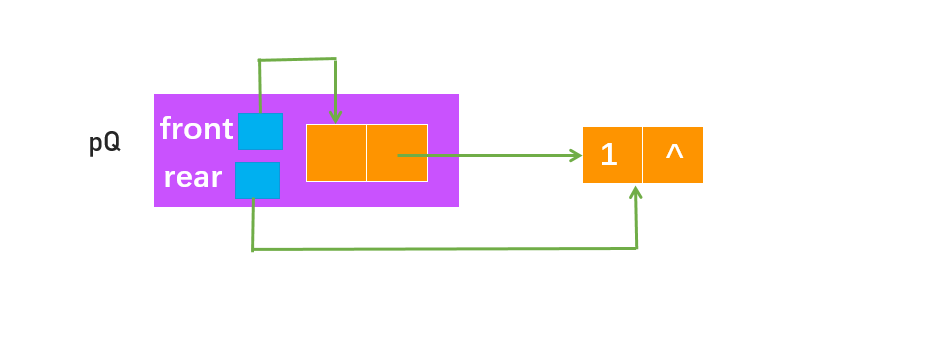
链式队列 一般定义为带头结点的单链表
为什么要带头结点?如图
结点定义:
1
2
3
4
5
6
7
8
9
10
11
12
13
| #define E int
typedef struct Node {
E data;
struct Node *next;
} LinkNode;
typedef struct {
LinkNode *front;
LinkNode *rear;
int size;
} LinkedQueue;
|
创建队列及相关操作:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
LinkedQueue *createQueue() {
LinkedQueue *pQ = (LinkedQueue *) malloc(sizeof(LinkedQueue));
pQ->front = pQ->rear = (LinkNode *) malloc(sizeof(LinkNode));
pQ->rear->next = NULL;
pQ->size = 0;
return pQ;
}
int getSize(LinkedQueue *pQ) {
return pQ->size;
}
int isEmpty(LinkedQueue *pQ) {
return 0 == pQ->size;
}
void printMessage(LinkedQueue *pQ) {
if (isEmpty(pQ)) {
printf("printMessage failed. LinkedQueue is empty.\n");
return;
}
printf("LinkedQueue: front ");
LinkNode * curNode = pQ->front->next;
while (curNode!=NULL){
printf("%d -> ", curNode->data);
curNode = curNode->next;
}
printf("rear \n");
}
|
入队:
1
2
3
4
5
6
7
8
9
|
void enQueue(LinkedQueue *pQ, E e) {
LinkNode *newNode = (LinkNode *) malloc(sizeof(LinkNode));
newNode->data = e;
newNode->next = NULL;
pQ->rear->next = newNode;
pQ->rear = newNode;
pQ->size++;
}
|
出队:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
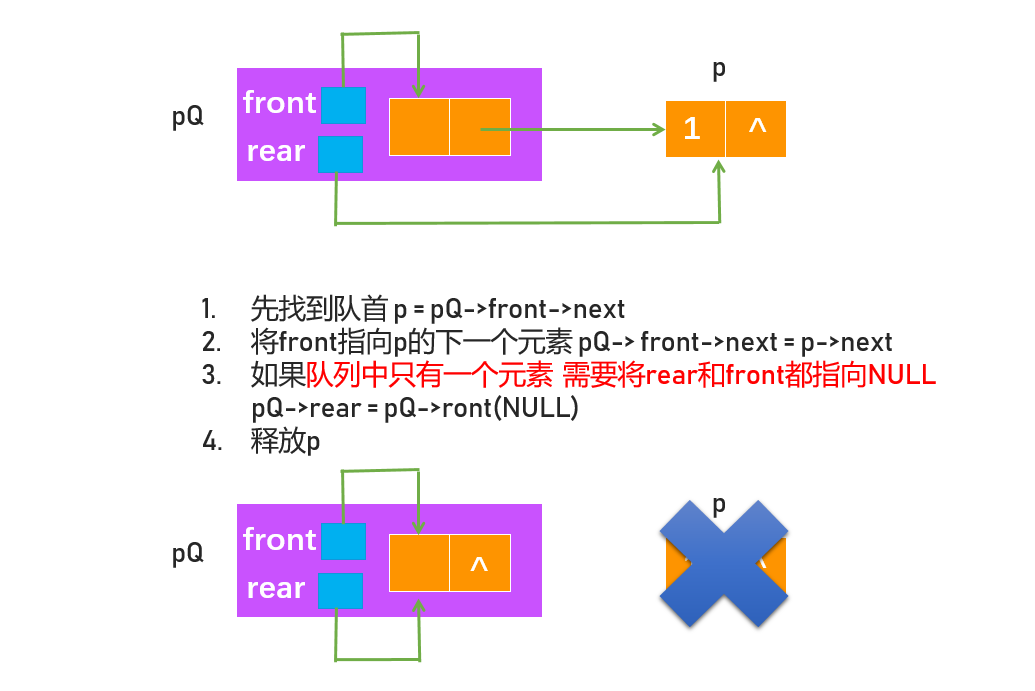
E deQueue(LinkedQueue *pQ) {
if (isEmpty(pQ)) {
printf("deQueue failed. LinkedQueue is empty.\n");
return -9999999;
}
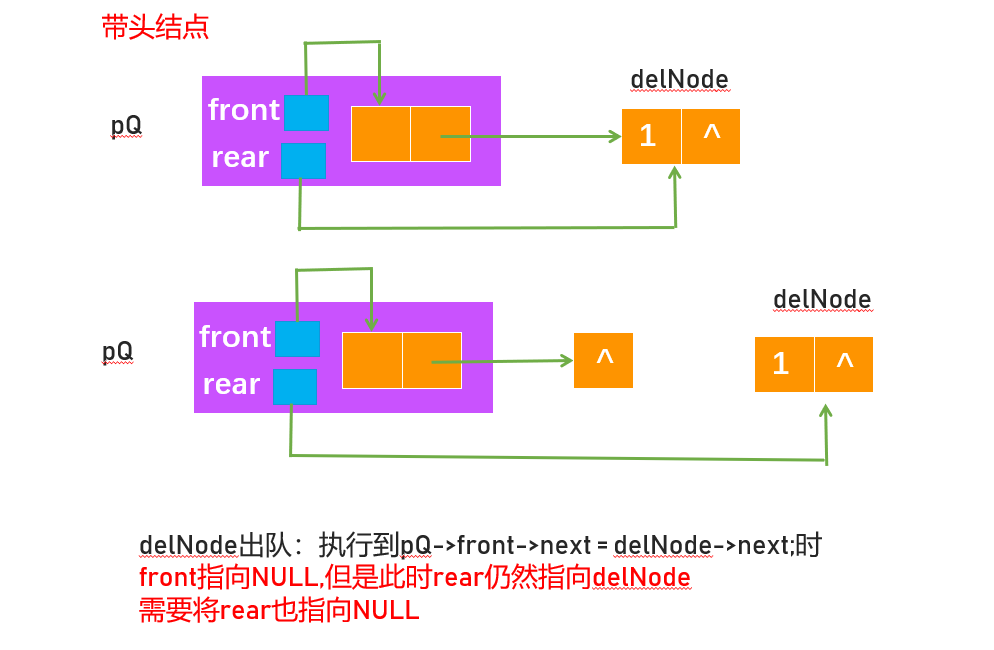
LinkNode *delNode = pQ->front->next;
E res = delNode->data;
pQ->front->next = delNode->next;
if (pQ->rear == delNode) {
pQ->rear = pQ->front;
}
free(delNode);
pQ->size--;
return res;
}
|
得到队头元素:
1
2
3
4
5
6
7
8
|
E getFront(LinkedQueue *pQ) {
if(isEmpty(pQ)){
printf("getFront failed. LinkedQueue is empty.\n");
return -9999999;
}
return pQ->front->next->data;
}
|
队列的基本应用-广度优先遍历
- 树:层序遍历
- 图:对无权图用广度优先遍历 就是最短路径
pS: 源代码链接