二分搜索树(二叉搜索树)

Algorithm


二分搜索树

  • 二叉树具有天然的递归结构，二分搜索树也是二叉树
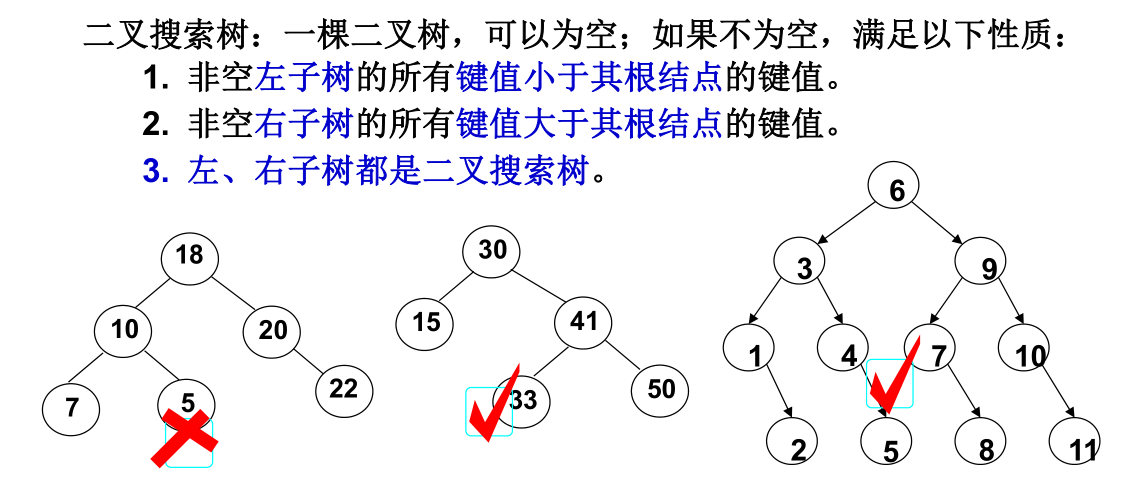
  • 二分搜索树的每个节点的值大于其左子树的所有节点的值，小于其右子树的所有节点的值
  • 每一颗子树也是二分搜索树
  • 存储的元素必须有可比较性
  • 一定是二叉树
  • 一定不会有相同的结点(考试的时候) 如果想要包含重复元素，只需要定义：左子树小于等于节点或者是右子树大于等于节点
  • 特点：对其中序遍历 可以得到一个 从小到大 的序列
  • 最小元素一定在最左边分支的端结点上 最大元素一定在最右边分支的端结点上
原理

节点构造：

1
2
3
4
5
6
7
8
9
10
#include <stdio.h>
#include <stdlib.h>

#define E int

typedef struct Node {
    E data;
    struct Node *left;
    struct Node *right;
} BSTNode;

二分搜索树 插入节点

我们的二分搜索树不包含重复元素 如果想要包含重复元素，只需要定义：左子树小于等于节点或者是右子树大于等于节点

新插入的节点总是叶子节点 插入data = 9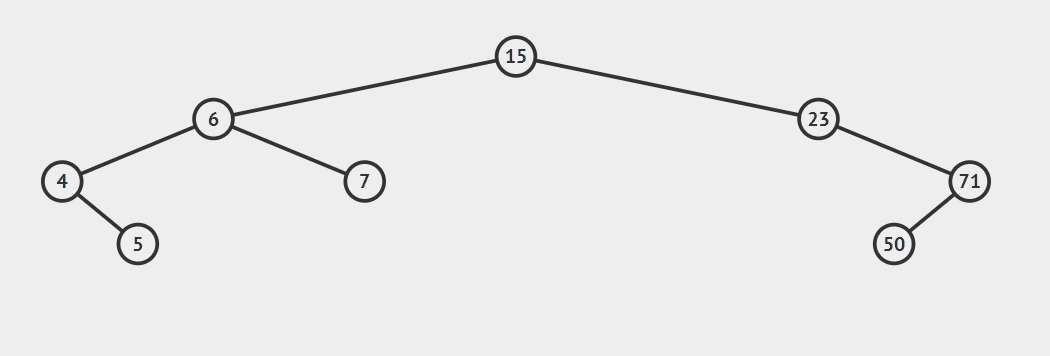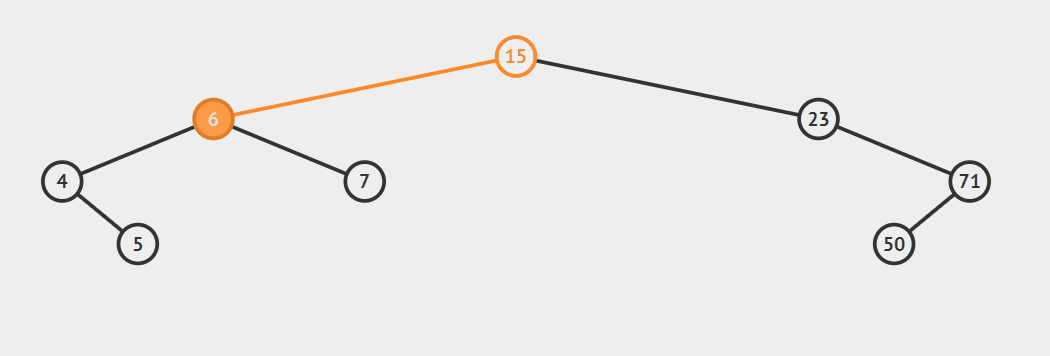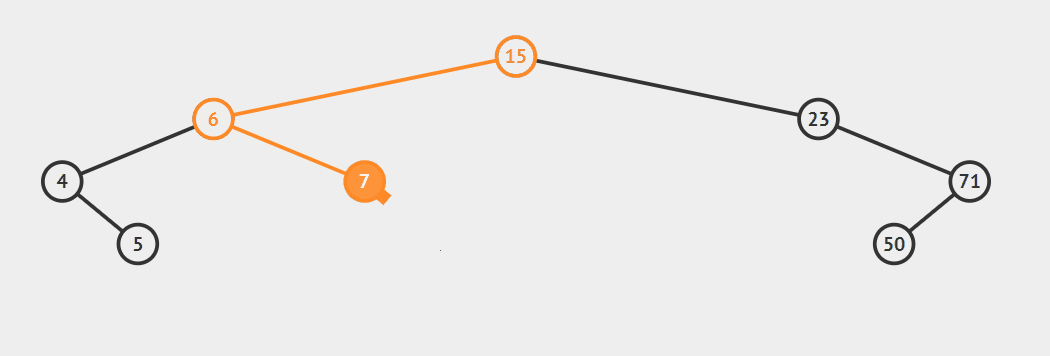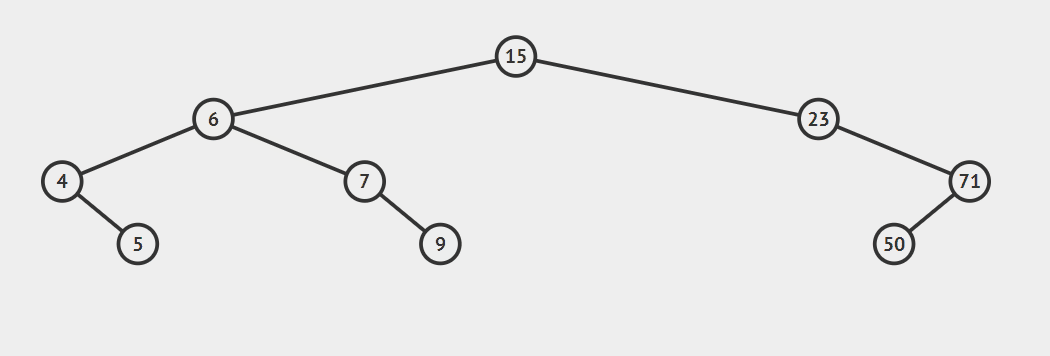
原理

基本思想：

1
2
3
4
5
6
7
8
9
10
/*
 * 插入结点  插入（找前驱）
 *   基本思想：
 *      1.如果二叉搜索树此时为空 则将插入结点当成新的根节点
 *      2.若二叉搜索树非空 从树根开始找 插入的值大于根结点 往根节点右边找
 *                                  插入的值小于根节点 往根节点左边找
 *                                  插入的值等于根节点 说明之前就有这个 值 结束插入
 *                                  直到为空NULL 此时找到了要插入结点的前驱结点
 *      3.若插入结点的值大于前驱结点 接到 前驱节点的右孩子域   小于前驱结点 接到左孩子域
 */

插入：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
// 插入 往二分搜索树中插入 数据
BSTNode * add(BSTNode * pT, E data){
    BSTNode *pre = NULL, *cur = NULL;  // cur:当前遍历到的节点  pre：cur的前驱

    BSTNode *newNode = (BSTNode *) malloc(sizeof(BSTNode)); // 创建 data节点并将左子域 右子域置NULL
    newNode->data = data;
    newNode->left = newNode->right = NULL;

    if (pT == NULL){    // 树空
        pT = newNode; // data所在的节点成为新的根节点
    }else {
        cur = pT; // 当前节点指向根节点  这样可以不改变根节点的地址
        while (cur != NULL) { // 遍历二分搜索树
            if (data < cur->data) { // data 比当前结点值小 去左子树找 并更新 pre cur的值
                pre = cur;
                cur = cur->left;
            } else if (data > cur->data) { // data 比当前结点值大 去右子树找 并更新 pre cur的值
                pre = cur;
                cur = cur->right;
            } else{ // data == cur->data  说明二分搜索树中已经有了这个节点 书上的二分索搜树是不包含重复元素的
                break; // 如果想包含重复元素 将break去掉加上 pre = cur; cur = cur->left?cur->left:cur->right;
                       // 并修改下面data < pre->data
                       // 想挂在重复节点的左孩子域  data < pre->data 改成 data <= pre->data
                       // 想挂在重复节点的右孩子域  data > pre->data 改成 data >= pre->data
            }
        }
        // 此时cur == NULL 说明找到了cur应在的位置 只需连接到其前驱节点就行了  插入的节点由于二分搜索树的特性都是 叶子节点
        if (data < pre->data) {
            pre->left = newNode;
        } else if (data > pre->data) {
            pre->right = newNode;
        }
    }
    return pT;
}

递归插入：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 向以pT为根的二分搜索树中插入节点
// 递归宏观语义：返回插入data后以data为根节点的二分搜索树
BSTNode *add_recursion(BSTNode *pT, E data) {
    if (pT == NULL) {     // 递归到最底层(包含树空的情况) 就是data节点应该在的位置
        // 创建data所在的节点
        BSTNode *newNode = (BSTNode *) malloc(sizeof(BSTNode));
        newNode->data = data;
        newNode->left = newNode->right = NULL;
        return newNode;
    }
    // 如果想包含重复元素 重复元素在左子域 data <= pT->data 在右子域 data >= pT->data
    if (data < pT->data) { // 如果data比当前节点小, 去左子树找,并更新左子树
        pT->left = add_recursion(pT->left, data);
    } else if (data > pT->data) {  // 如果data比当前节点大,去右子树找,并更新右子树
        pT->right = add_recursion(pT->right, data);
    }  // data = pT->data 因为我们写的二分搜索树不包含重复元素 所以此处不做任何操作
    return pT;  // 此处一定要返回pT  画图体会
}

二分搜索树创建 基于插入算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
// 创建二分搜索树 基于 插入元素
BSTNode * createBST(E * nums, int len){
    BSTNode *pT = NULL;         // 这里不能malloc 初始为空
    int i;
    for (i = 0; i < len; ++i) {
        pT = add(pT, nums[i]);
    }
    return pT;
}

int main(void) {
    int len = 5;
    E nums[len] = {5, 4, 20, 17, 18};
    BSTNode * bst = createBST(nums, len);
}

二分搜索树 前序 中序 后序遍历(深度优先)

前序遍历： 根 -> 左 -> 右
中序遍历： 左 -> 根 -> 右
后序遍历： 左 -> 右 -> 根

递归算法:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 递归宏观语义：求以pT为根节点的二分搜索树的前序遍历
void preOrder_recursion(BSTNode *pT) {
    if (pT == NULL) {   // 递归到最底层  树空
        return;
    }
    printf("%d ", pT->data);        // 打印根节点
    preOrder_recursion(pT->left);     // 递归遍历左子树
    preOrder_recursion(pT->right);    // 递归遍历右子树
}

// 递归宏观语义：求以pT为根节点的二分搜索树的中序序遍历
void inOrder_recursion(BSTNode *pT) {
//    if (pT == NULL) {   // 递归到最底层  树空
//        return;
//    }
    if (pT) {
        inOrder_recursion(pT->left);     // 递归遍历左子树
        printf("%d ", pT->data);        // 打印根节点
        inOrder_recursion(pT->right);    // 递归遍历右子树
    }
}

// 递归宏观语义：求以pT为根节点的二分搜索树的后序遍历
void postOrder_recursion(BSTNode *pT) {
    if (pT == NULL) {   // 递归到最底层  树空
        return;
    }
    postOrder_recursion(pT->left);     // 递归遍历左子树
    postOrder_recursion(pT->right);    // 递归遍历右子树
    printf("%d ", pT->data);        // 打印根节点
}

非递归算法：适用于先序 中序 后序：利用栈模拟系统栈实现非递归：点击这里
借助栈 栈的内容如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
// 栈的节点定义以及操作  
typedef struct node {
    char *s;              // 二分搜索树结点的描叙性信息 go：访问 print：打印
    BSTNode* data;        // 二分搜索树节点
    struct node *Next;
} StackNode;

typedef struct Stack {
    StackNode *pTop;
} LinkStack;

LinkStack *createStack() { // 创建栈
    LinkStack *pS = (LinkStack *) malloc(sizeof(LinkStack));
    pS->pTop = NULL;
}

void push(LinkStack *pS, char *s, BSTNode* data) { // 入栈 压入 该节点的描叙字符 和 该节点
    StackNode *newNode = (StackNode *) malloc(sizeof(StackNode));
    newNode->Next = pS->pTop;
    newNode->s = s;
    newNode->data = data;
    pS->pTop = newNode;
}

int emptyStack(LinkStack *pS) { // 判断栈是否为空
    return pS->pTop == NULL;
}

void pop(LinkStack *pS, char **s, BSTNode **data) { // 出栈
    if (pS->pTop == NULL) {
        return;
    }
    StackNode *temp = pS->pTop;
    *s = temp->s;
    *data = temp->data;
    pS->pTop = temp->Next;
    free(temp);
    return;
}

非递归遍历通用算法：模拟系统栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
// 非递归先序遍历
void preOrder(BSTNode *pT) {
    LinkStack *stack = createStack();
    char *s = NULL;   // s : 入栈的这个指令的信息 "go":访问这个节点   "print":打印这个节点的值
    BSTNode *node = NULL;
    push(stack, "go", pT);  // 根节点入栈
    while (!emptyStack(stack)) { // 栈不空
        pop(stack, &s, &node); // 取出栈顶节点 看有什么指令
        if (s == "print") { // 打印其节点值
            printf("%d ", node->data);
        } else{ // s == "go" 访问
            if (node->right != NULL) {               // ①   访问右子树 右
                push(stack, "go", node->right);
            }
            if (node->left != NULL) {                // ②   访问左子树 左
                push(stack, "go", node->left);
            }
            push(stack, "print", node);              // ③   访问根节点 根
            // 因为栈的特性 后进先出  入栈顺序 右-> 左 -> 根 对应实际执行顺序 根 -> 左 -> 右 (先序)
            //                      入栈顺序 右-> 根 -> 左 对应实际执行顺序 左 -> 根 -> 右 (中序)
            //                      入栈顺序 根-> 右 -> 左 对应实际执行顺序 左 -> 右 -> 根 (后序)
        }
    }
}

原理

二分搜索树 层次遍历(广度优先遍历)

基本思想：

1
2
3
4
5
6
/*
 * 层次遍历 广度优先遍历 队列
 *   基本思想： 从整个树的根节点开始 如果树不为空 将根节点入队
 *             如果队列不为空 出队  打印出队元素的值
 *             如果出队元素左孩子不为空 入队  右孩子不为空 入队  直到队列为空为止
 */

借助队列：队列内容如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
// 队列的节点定义以及操作
typedef struct qnode{
    BSTNode * data;         // 数据域存放的是 BSTnode节点
    struct qnode *next;
}QueueNode;

typedef struct {
    QueueNode * front;
    QueueNode * rear;
}LinkQueue;

LinkQueue * createQueue(){
    LinkQueue *pQ = (LinkQueue *) malloc(sizeof(LinkQueue));
    pQ->front = pQ->rear = (QueueNode *) malloc(sizeof(QueueNode));
    pQ->rear->next = NULL;
    return pQ;
}

void addQueue(LinkQueue * pQ, BSTNode * node){
    QueueNode *newNode = (QueueNode *) malloc(sizeof(QueueNode));
    newNode->data = node;
    newNode->next = NULL;
    pQ->rear->next = newNode;
    pQ->rear = newNode;
}

int emptyQueue(LinkQueue * pQ){
    return pQ->front == pQ->rear;
}
BSTNode * removeQueue(LinkQueue * pQ){
    if (emptyQueue(pQ)) { // 队列空
        return NULL;
    }
    QueueNode *temp = pQ->front->next;
    BSTNode *data = temp->data;
    pQ->front->next = temp->next;
    if (temp == pQ->rear) { // 队列中只有一个节点 被删除的情况
        pQ->rear = pQ->front ;
    }
    return data;
}

层次遍历：广度优先

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 层次遍历 借用队列  (广度优先遍历)
void levelOrder(BSTNode *pT){
    if (pT == NULL) { // 二分搜索树空
        return;
    }
    LinkQueue *queue = createQueue();
    addQueue(queue, pT);  // 根节点入队
    while (!emptyQueue(queue)) { // 队列不空
        BSTNode *node = removeQueue(queue); // 取出队首节点
        printf("%d ", node->data);  // 打印
        if (node->left != NULL) {  // 左子树不空 压入队列
            addQueue(queue, node->left);
        }
        if (node->right != NULL) { // 右子树不空 压入队列
            addQueue(queue, node->right);
        }
    }
}

二分搜索树 查找元素

基本思想：

1
2
3
4
5
6
7
/*
 * 查找data 所在的位置(地址)
 *    基本思想：从树根开始找 如果data比根节点的data大 往根节点右边找
 *                         如果data比根节点的data小 往根节点左边找
 *                         如果data == 根结点的data  找到了
 *                         如果上述情况都不是 则不存在data这个结点
 */

查找：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
// 查找元素data的位置
BSTNode *find(BSTNode *pT, E data) {
    if (pT == NULL) {   // 树空
        return NULL;
    } /* else {
        BSTNode *cur = pT;
        while (cur != NULL) {
            if (data < cur->data) {
                cur = cur->left;
            } else if (data > cur->data) {
                cur = cur->right;
            } else { // data == cur_>data 找到了
                return cur;
            }
        }
    }*/
    // 上面的写法可以换种形式 更简洁
    BSTNode *cur = pT;
    while (cur != NULL){
        if (data == cur->data) { // 找到了
            return cur;
        }
        cur = data < cur->data ? cur->left : cur->right;
    }
    return NULL; // 没有找到
}

递归算法:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
// 查找元素data
// 递归宏观语义: 返回在以pT为根的二分搜索树中 含有data的节点的地址
BSTNode * find(BSTNode * pT, E data){
    if (pT == NULL){    // 递归到底 发现都没找到data
        return NULL;
    }
    if (data == pT->data) { // 找到了 返回
        return pT;
    } else if (data < pT->data) { // data小于当前节点的值 去左子树找
        return find(pT->left, data);
    } else{  // data 大于当前节点的值 去右子树找
        return find(pT->right, data);
    }
}

二分搜索树 查最大值

基本思想：

1
2
3
4
/*
 * 查找最大值：
 *     基本思想：一路从根节点往右边查 直到 为空  最右边那个结点就是最大值
 */

查找最大值节点：

1
2
3
4
5
6
7
8
9
10
11
// 查找最大值节点
BSTNode *findMax(BSTNode *pT){
    if (pT == NULL) {
        return NULL;
    }
    BSTNode *cur = pT;
    while (cur->right != NULL) {  // 沿右分支一直向下，直到最右端点
        cur = cur->right;
    }
    return cur;
}

递归：

1
2
3
4
5
6
7
8
// 查找最大值 递归算法
// 递归宏观语义: 返回以pT为根的二分搜索树的最大值所在的节点
BSTNode *findMax_recursion(BSTNode *pT){
    if (pT->right == NULL) {
        return pT;
    }
    return findMax_recursion(pT->right);
}

二分搜索树 查最小值节点

基本思想：

1
2
3
4
/*
 * 查找最小值：
 *     基本思想：一路从根节点往左边查 直到 为空  最左边那个结点是最小值
 */

查找最小值节点：

1
2
3
4
5
6
7
8
9
10
11
// 查找最小值节点
BSTNode *findMin(BSTNode *pT){
    if (pT == NULL) {
        return NULL;
    }
    BSTNode *cur = pT;
    while (cur->left != NULL) {  // 沿左分支一直向下，直到最左端点
        cur = cur->left;
    }
    return cur;
}

递归：

1
2
3
4
5
6
7
8
// 查找最小值 递归算法
// 递归宏观语义: 返回以pT为根的二分搜索树的最小值所在的节点
BSTNode *findMin_recursion(BSTNode *pT){
    if (pT->left == NULL) {
        return pT;
    }
    return findMin_recursion(pT->left);
}

二分搜索树 删除最小值节点

递归:

1
2
3
4
5
6
7
8
9
10
11
12
// 递归删除最小值节点
// 返回删除最小值后 新的二分搜索树的根
BSTNode *removeMin_recursion(BSTNode *pT) {
    if (pT->left == NULL) { // 递归到底
        BSTNode *rightNode = pT->right;
        pT->right = NULL;
        free(pT);
        return rightNode;
    }
    pT->left = removeMin_recursion(pT->left);
    return pT;
}

二分搜索树 删除任意节点

基本思想：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/*
 * 删除结点
 *    基本思想：
 *    * 删除结点 3种情况
 *    1.删除的是叶子节点
 *        将其父节点对应的指针域 设为NULL
 *    2.删除的结点 只有一颗左子树或右子树
 *        用子树的根节点取代被删除结点
 *    3.删除的结点 有左右两颗子树  （2种方法）
 *        1）中序直接前驱法：将被删除结点的中序遍历的直接前驱结点 取代删除结点
 *        2）中序直接后继法：将被删除结点的中序遍历的直接后继结点 取代删除结点
 *        找被删除点的前驱：从被删除点的左子树 一路向右  (被删结点左子树中的最大值)
 *        找被删除点的后继：从被删除点的右子树 一路向左  (被删结点右子树中的最小值)
 */

删除只有左孩子的节点： 将节点58左子树的根节点50取代待删除节点

原理

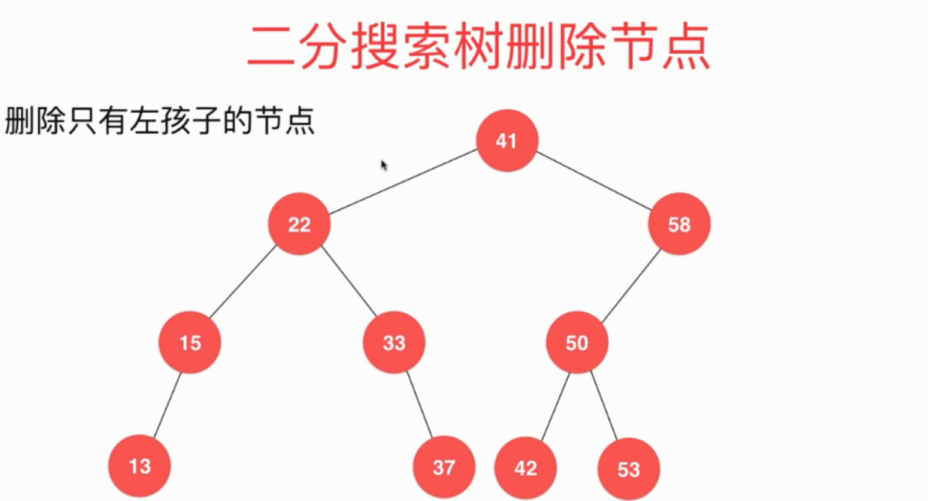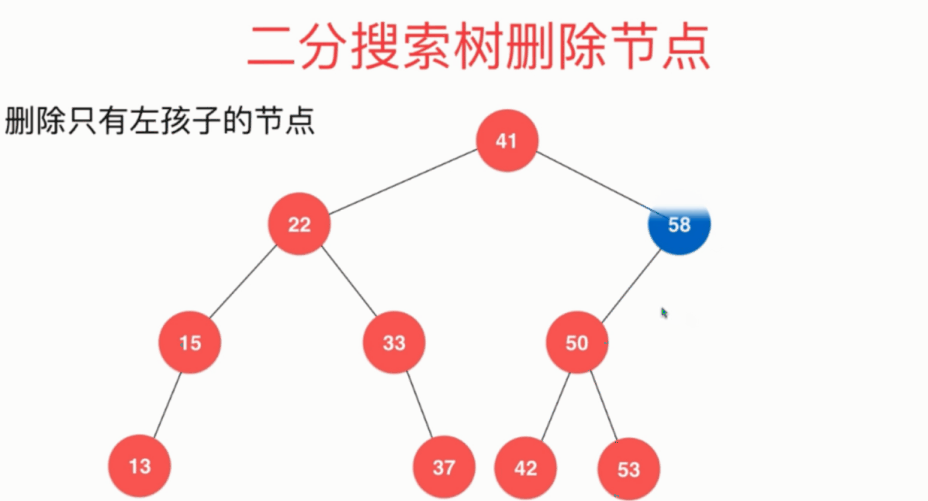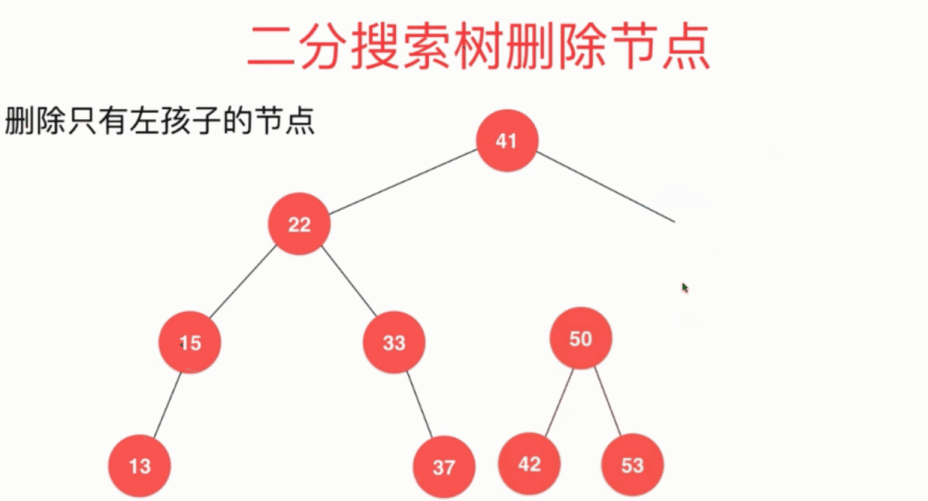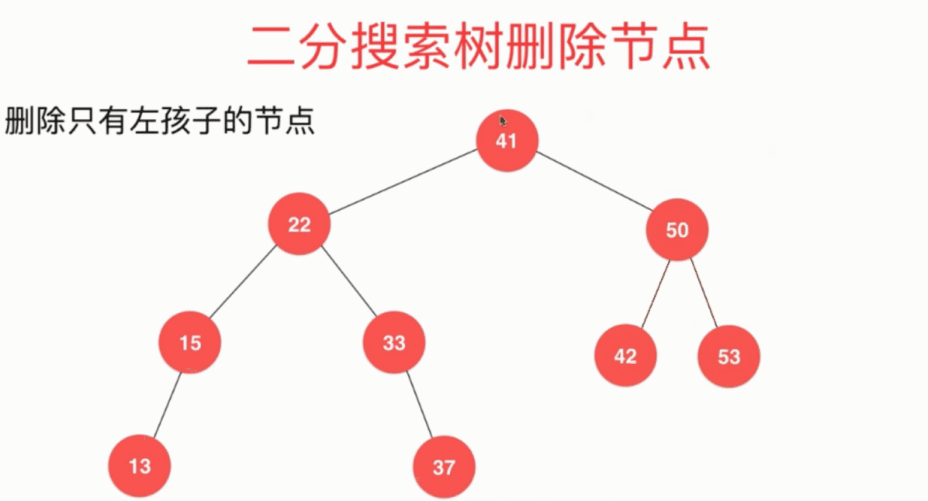
删除只有右孩子的节点： 将节点58右子树的根节点60取代待删除节点

原理

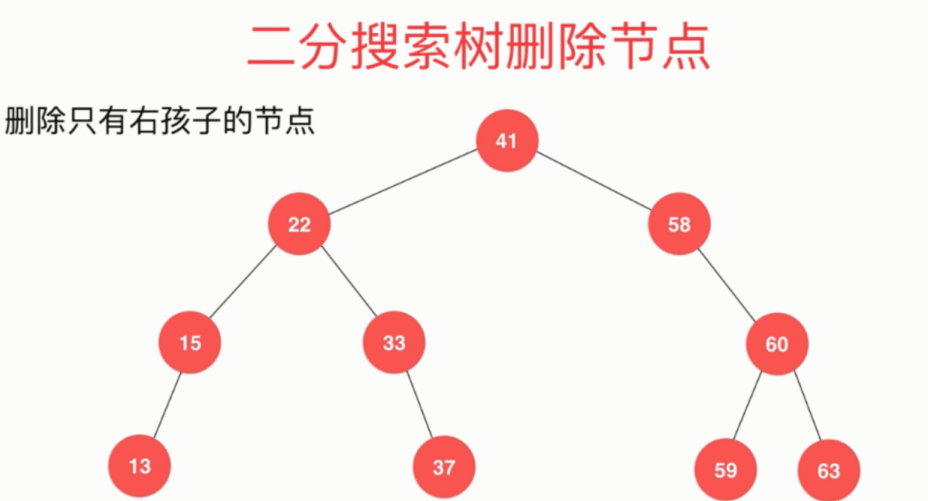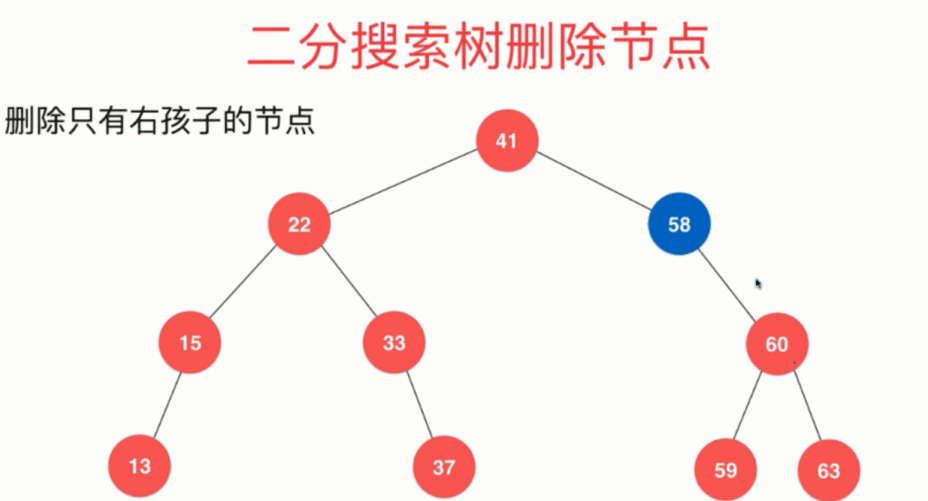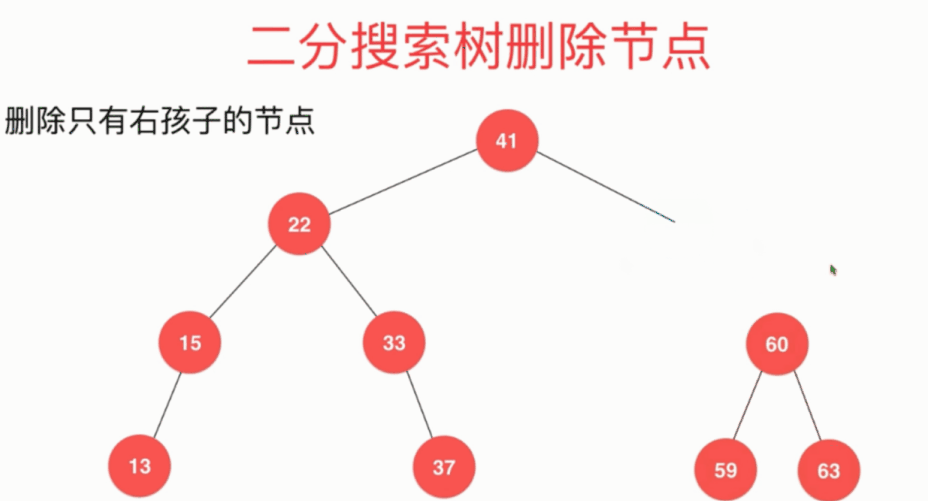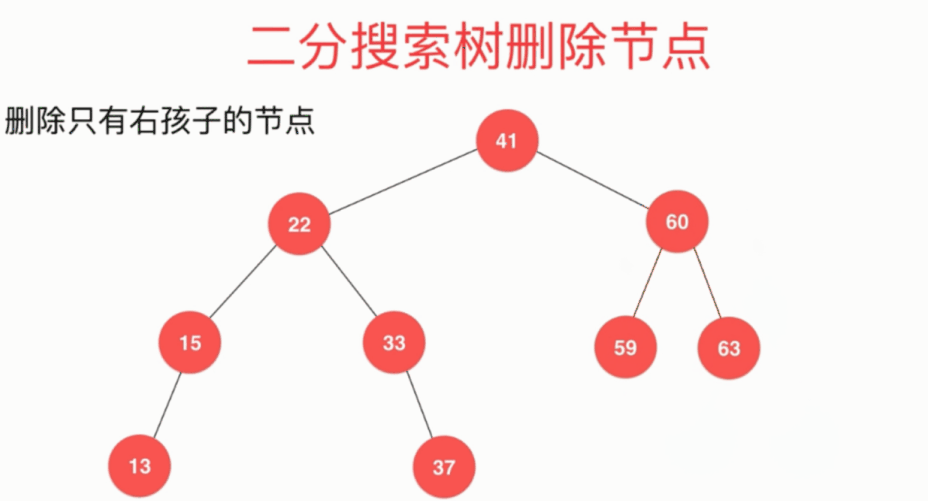
删除有左右子树的节点 删除28 动画演示如下： 中序直接后继法

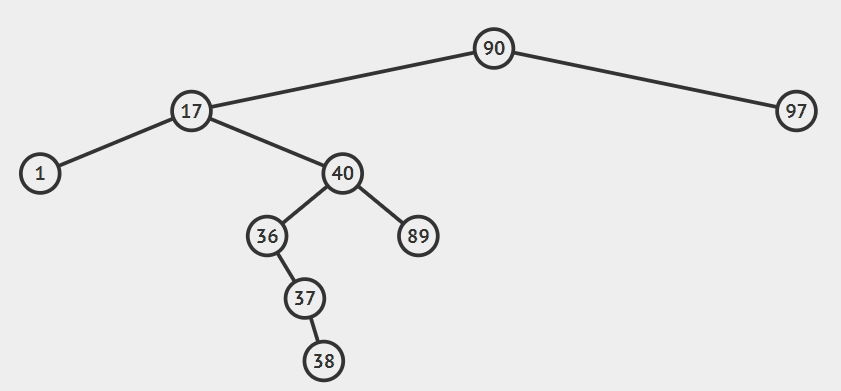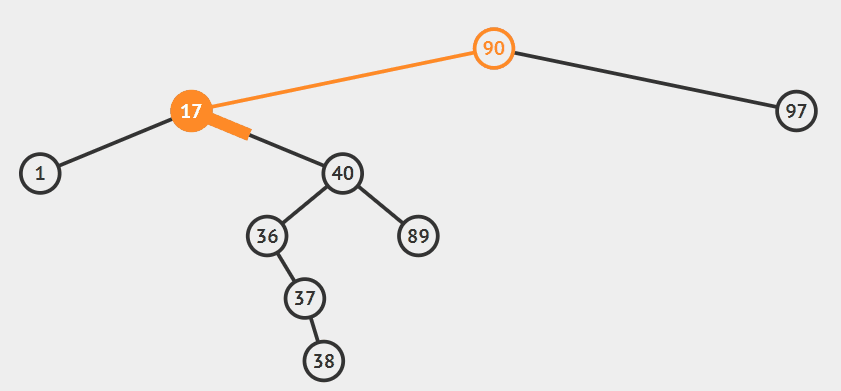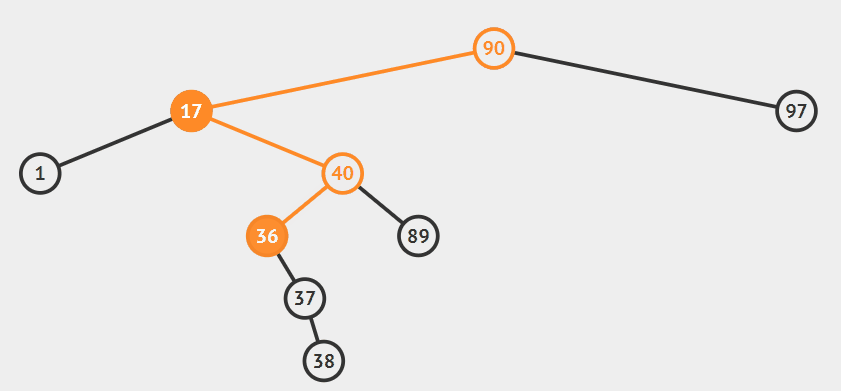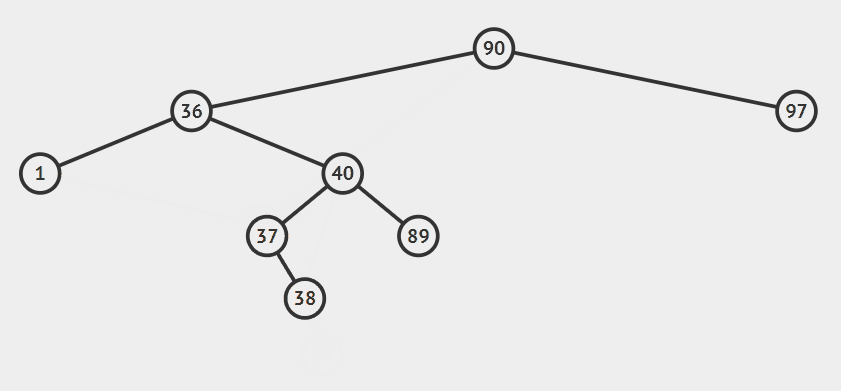
  1. 采用中序直接后继法（中序直接前驱法一样的道理只是去找待删除节点左子树的最大值取代待删除节点
  2. 在待删除节点17右子树找到的最小值节点36(找到待删除节点的直接后继)
  3. 将最小值36的右子树的根节点37挂到36的父亲节点对应的位置
  4. 并将最小值节点36取代待删除节点，其右孩子指向待删除节点的右子树(此时右子树已经删除了最小值节点)，左孩子指向待删除节点的左子树，最后删掉待删除节点17
原理

删除任意节点：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
// 递归删除最大值节点
// 返回删除最大值后 新的二分搜索树的根
BSTNode *removeMax_recursion(BSTNode *pT) {
    if (pT->right == NULL) { // 递归到底
        BSTNode *leftNode = pT->left;
        pT->left = NULL;
        free(pT);
        return leftNode;
    }
    pT->right = removeMax_recursion(pT->right);
    return pT;
}

// 删除掉以pT为根的二分搜索树中值为data的节点, 递归算法
// 返回删除节点后新的二分搜索树的根
BSTNode *remove_recursion(BSTNode *pT, E data) {
    if (pT == NULL) {   // 没有data这个节点
        return NULL;
    }
    if (data < pT->data) { // 去左子树递归删除
        pT->left = remove_recursion(pT->left, data);
        return pT;
    } else if (data > pT->data) { // 去右子树递归删除
        pT->right = remove_recursion(pT->right, data);
        return pT;
    } else { // data == pT->data 找到了data节点
        if (pT->left == NULL) { // 有右子树 || 左右子树都没有
            BSTNode *rightNode = pT->right;
            pT->right = NULL;
            free(pT);
            return rightNode;
        }
        if (pT->right == NULL) { // 只有左子树
            BSTNode *leftNode = pT->left;
            pT->left = NULL;
            free(pT);
            return leftNode;
        }
        // 待删除节点左右子树均不为空的情况
        // 用中序直接后继法去右子树找到最小值节点 用它取代待删除节点
        BSTNode *successor = findMin(pT->right);
        // 这里也可以写成successor->right = remove_recursion(pT->right，successor->data);
        successor->right = removeMin_recursion(pT->right);
        successor->left = pT->left;
        pT->left = pT->right = NULL;
        free(pT);
        return successor;
    }
}

leetcode对应习题

  1. Delete Node in a BST:题目链接
  2. Kth Smallest Element in a BST:题目链接

本文标题:二分搜索树(二叉搜索树)

文章作者:XerDemo

发布时间:2018-11-25, 10:49:11

最后更新:2019-02-13, 18:13:04

原始链接:https://xerdemo.github.io/2018/11/25/二叉搜索树C版/

许可协议: "署名-非商用-相同方式共享 4.0" 转载请保留原文链接及作者。

文章目录
  1. 1. 二分搜索树
  2. 2. 二分搜索树 插入节点
  3. 3. 二分搜索树创建 基于插入算法
  4. 4. 二分搜索树 前序 中序 后序遍历(深度优先)
  5. 5. 二分搜索树 层次遍历(广度优先遍历)
  6. 6. 二分搜索树 查找元素
  7. 7. 二分搜索树 查最大值
  8. 8. 二分搜索树 查最小值节点
  9. 9. 二分搜索树 删除最小值节点
  10. 10. 二分搜索树 删除任意节点
|