栈的特点:后进先出 Last In First Out(LIFO)
相比数组,栈对应的操作是数组的子集
只能从栈顶添加元素,删除元素
顺序栈-动态数组
节点定义:1
2
3
4
5// 不能动态伸缩数组的节点定义
typedef struct {
E data[capacity];
int top;
} ArrayStack;
1 |
|
相关操作:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41// 初始化栈 top等于-1时 表示栈空 top等于MAXSIZE-1时 表示栈满
ArrayStack *initStack() {
ArrayStack *stack = (ArrayStack *) malloc(sizeof(ArrayStack));
stack->data = (E *) malloc(sizeof(E) * INITSIZE);
stack->capacity = INITSIZE;
stack->top = -1;
return stack;
}
// 顺序栈是否为空
int isEmpty(ArrayStack *stack) {
return -1 == stack->top;
}
// 获取顺序栈中元素个数
int getSize(ArrayStack *stack) {
return stack->top + 1;
}
// 获取顺序栈的最大容量
int getCapacity(ArrayStack *stack) {
return stack->capacity;
}
// 打印栈信息
void printMessage(ArrayStack *stack){
if (isEmpty(stack)){
printf("printMessage failed. stack is empty.\n");
return ;
}
printf("Array:size = %d , capacity = %d \n", getSize(stack), getCapacity(stack));
int i;
printf("stack : [");
for (i = 0; i <= stack->top; ++i) {
printf("%d", stack->data[i]);
if (i != stack->top) {
printf(", ");
}
}
printf("] top\n");
}
入栈:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19// 将数组空间的容量扩容成newCapacity大小 O(1)
void resize(ArrayStack *stack, int newCapacity) {
E *newData = (E *) malloc(sizeof(E) * newCapacity);
int i;
for (i = 0; i <= stack->top; ++i) {
newData[i] = stack->data[i];
}
stack->data = newData;
stack->capacity = newCapacity;
}
// 入栈 不算resize() O(1)
void push(ArrayStack *stack, E e) {
if (stack->top + 1 == stack->capacity) { // 栈满
resize(stack, 2 * stack->capacity);
}
stack->top++;
stack->data[stack->top] = e;
}
出栈:1
2
3
4
5
6
7
8
9
10
11
12
13// 出栈 并返回出栈元素 O(1) 并没有真正的删除栈顶元素 只是改变了栈顶指针的指向
E pop(ArrayStack *stack) {
if (isEmpty(stack)){
printf("pop failed. stack is empty.\n");
return -9999999;
}
E res = stack->data[stack->top];
stack->top--;
if (stack->top + 1 == stack->capacity / 2) {
resize(stack, stack->capacity / 2);
}
return res;
}
获取栈顶元素:1
2
3
4
5
6
7
8// 获取栈顶元素 O(1)
E peek(ArrayStack *stack){
if (isEmpty(stack)){
printf("peek failed. stack is empty.\n");
return -9999999;
}
return stack->data[stack->top];
}
链式栈
首先链式栈 一般都定义为 有结构体包着 并且 只有头指针 没有头结点节点定义如下:1
2
3
4
5
6
7
8
9
10
// 链式栈节点定义
typedef struct stackNode{
E data; // 数据域
struct stackNode * next; // 指针域
}StackNode;
typedef struct {
StackNode * top; // 栈顶指针
}LinkStack;
为什么会这样定义呢?看下面几种情况
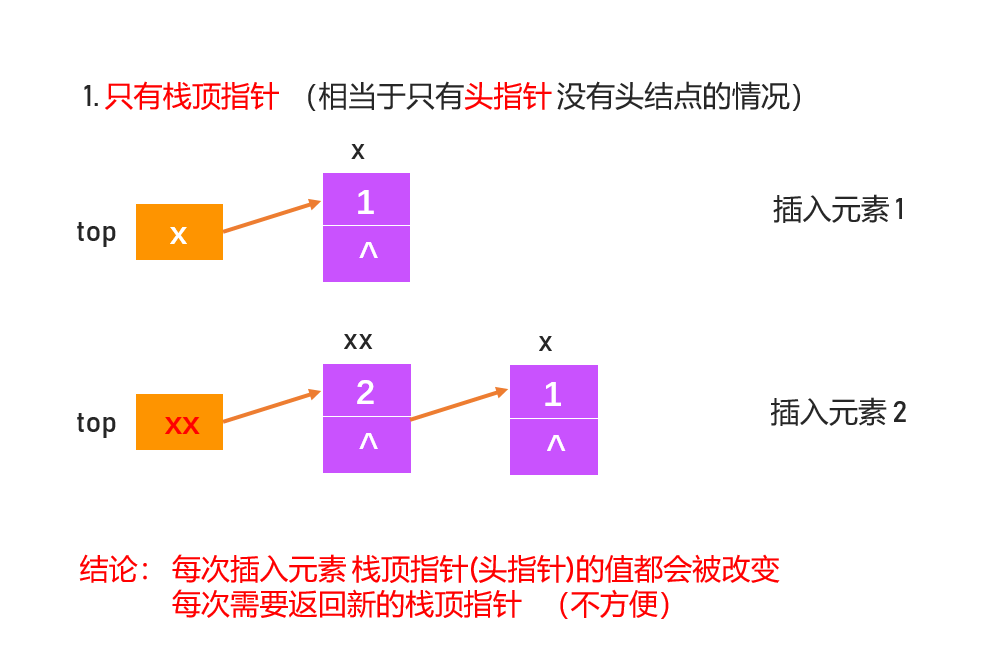
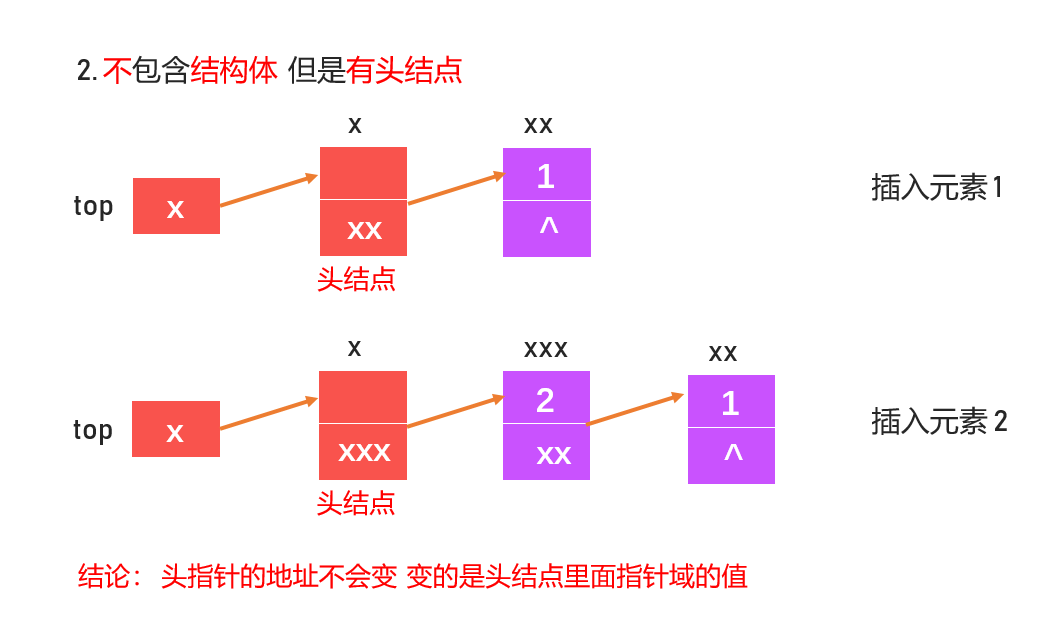
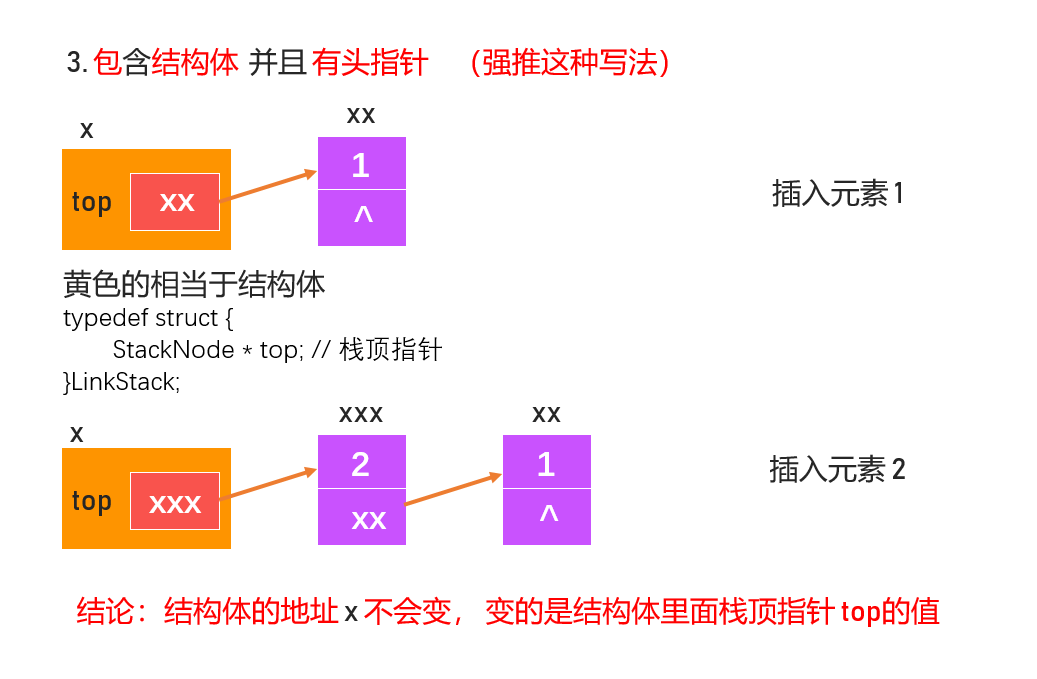
LinkedStack.c1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
// 链式栈节点定义
typedef struct stackNode{
E data; // 数据域
struct stackNode * next; // 指针域
}StackNode;
typedef struct {
StackNode * top; // 栈顶指针
int size; // 栈中元素个数 加入size变量可以使求长度操作的复杂度从O(N)降为O(1)
// 不需要遍历求链栈长度 只需要花费一点时间维护size
}LinkedStack;
// 创建链栈
LinkedStack * createStack(){
LinkedStack *stack = (LinkedStack *) malloc(sizeof(LinkedStack));
if (stack == NULL) {
printf("malloc is failed.\n");
exit(-1);
}
stack->top = NULL;
stack->size = 0;
return stack;
}
// 获取链式栈大小 O(1)
int getSize(LinkedStack * stack){
return stack->size;
}
//// 链栈的长度 O(N) 不加size时
//int getSize(LinkStack * stack){
// stackNode * curNode = stack->top;
// int count = 0;
// while (curNode->next != NULL) {
// count++;
// curNode = curNode->next;
// }
// return count;
//}
// 返回链式栈是否为空 O(1)
int isEmpty(LinkedStack * stack){
return 0 == stack->size;
}
// 入栈 O(1)
void push(LinkedStack * stack, E data){
StackNode *newNode = (StackNode *) malloc(sizeof(StackNode));
newNode->data = data;
newNode->next = stack->top;
stack->top = newNode;
stack->size++;
}
// 出栈 O(1)
E pop(LinkedStack * stack){
if (isEmpty(stack)){
printf("LinkStack is empty, pop is failed.\n");
return ERROR;
}
StackNode * delNode = stack->top; // 待出栈节点
E res= delNode->data; // 出栈节点的数据域
stack->top = delNode->next; // 栈顶指针指向待出栈节点的后一个节点
free(delNode); // 释放待出栈节点
delNode = NULL;
stack->size--;
return res;
}
// 获取栈顶元素 O(1)
E peek(LinkedStack * stack){
if (isEmpty(stack)){
printf("peek failed. LinkedStack is empty.\n");
return -9999999;
}
return stack->top->data;
}
// 打印栈信息
void printMessage(LinkedStack * stack){
if (isEmpty(stack)){
printf("printMessage failed. LinkedStack is empty.\n");
return;
}
StackNode * curNode = stack->top;
printf("LinkedStack is: top ");
while (curNode != NULL) {
printf("%d -> ", curNode->data);
curNode = curNode->next;
}
printf("NULL \n");
}
int main(void) {
LinkedStack *stack = createStack();
int i;
for (i = 0; i < 5; ++i) {
push(stack, i);
}
printf("size: %d peek: %d\n", getSize(stack), peek(stack));
printMessage(stack);
printf("------------\n");
printf("pop: %d\n",pop(stack));
printf("size: %d peek: %d\n", getSize(stack), peek(stack));
printMessage(stack);
printf("------------\n");
return 0;
}
栈的应用
- undo操作(撤回) - 编译器
- 系统调用栈 - 操作系统
- 括号匹配 - 编译器