堆
最大堆?最小堆?
最大堆:堆中每个节点的值>=子节点的值最小堆:堆中每个节点的值<=子节点的值- 堆总是一颗完全二叉树
- 为什么用数组来实现堆?
二叉堆是一个完全二叉树 把完全二叉树编号后 编号就可以对应数组中的索引
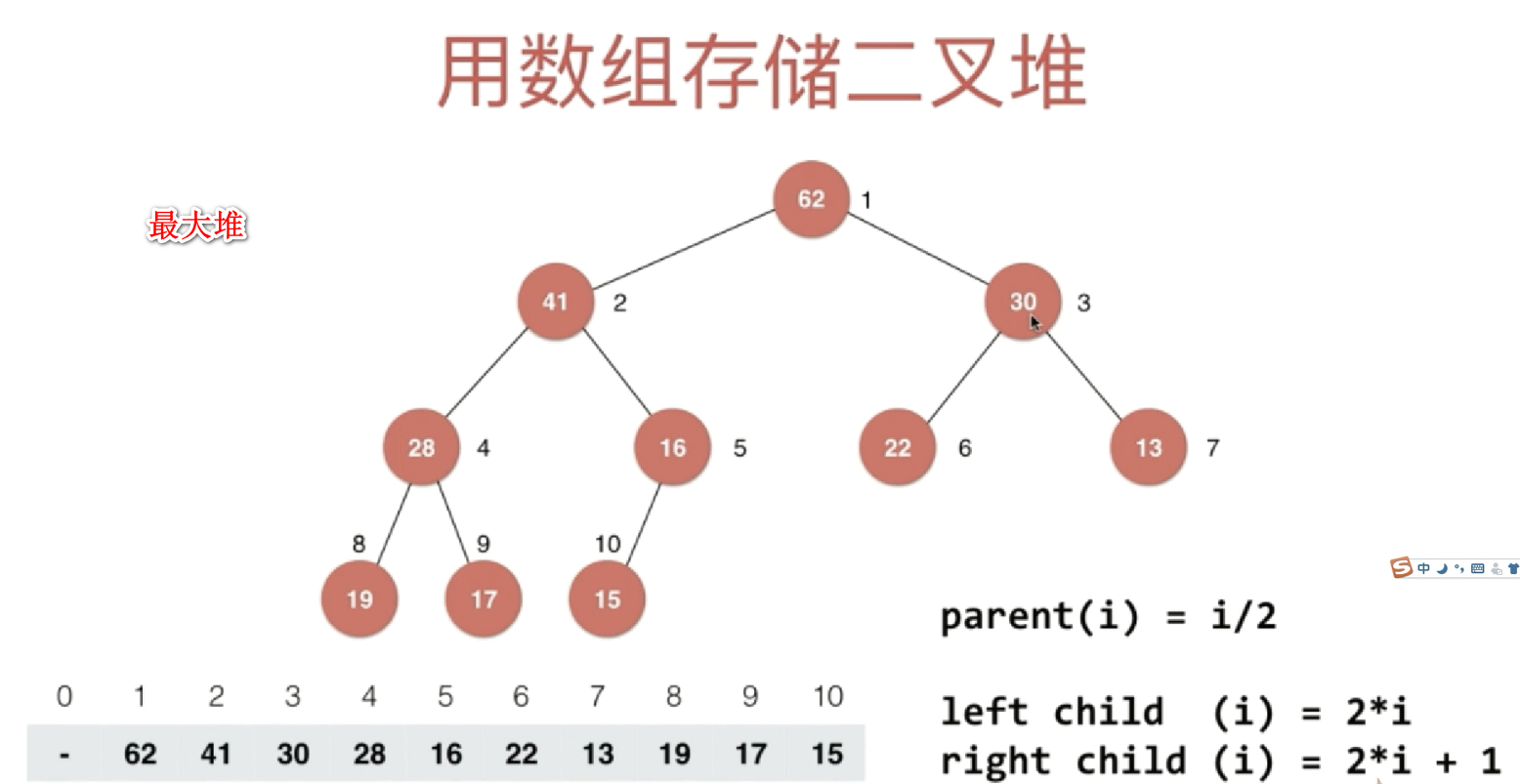
如果从1开始编号,父节点 = 当前节点索引 / 2,左孩子 = 当前节点索引 * 2,右孩子 = 当前节点索引 *2 + 1
从1开始编号,用数组来表示一颗完全二叉树,最后一个非叶子节点索引:最后一个节点索引/2,
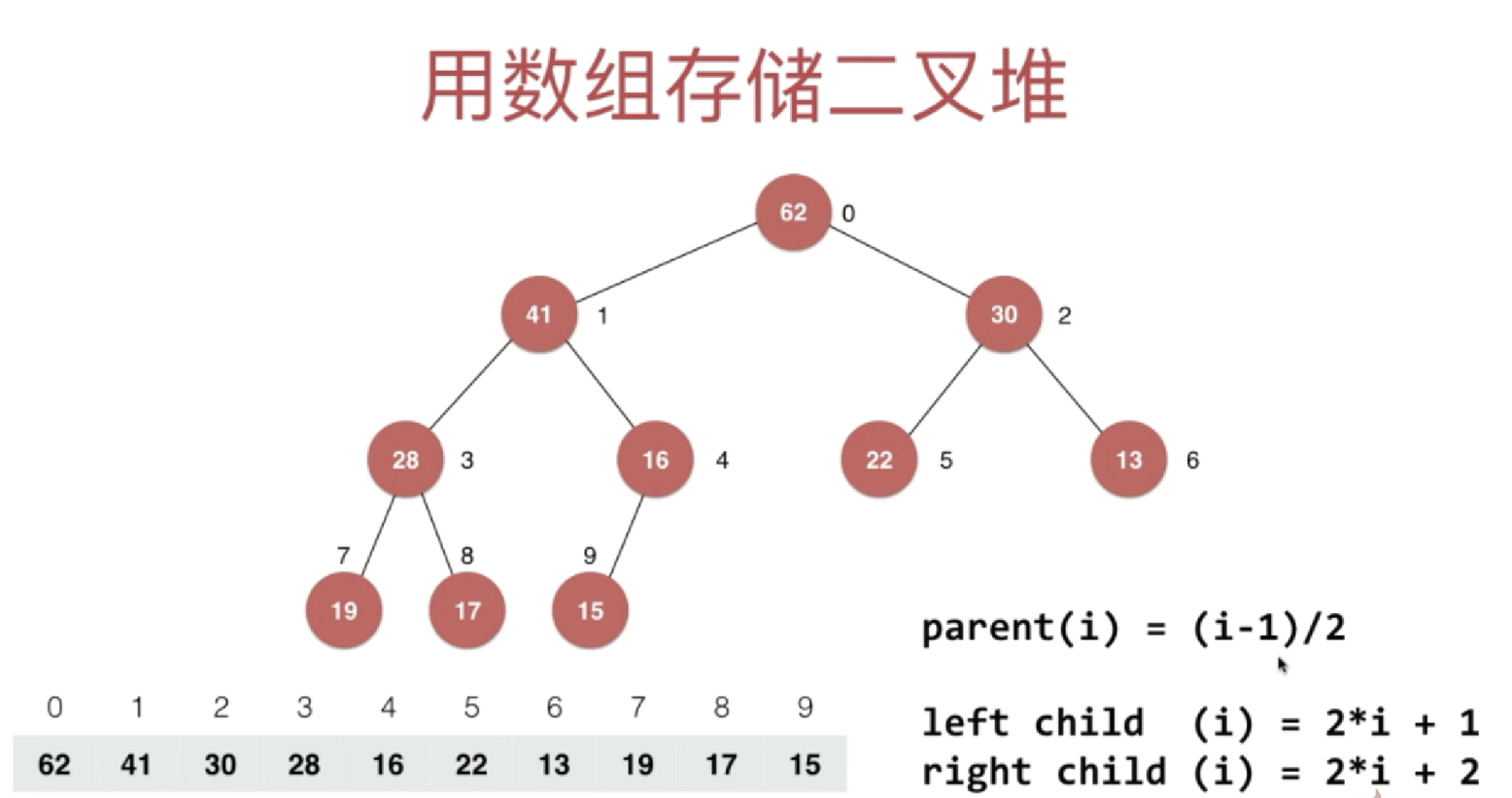
如果从0开始编号,父节点 = (当前节点索引-1) / 2 , 左孩子 = 当前节点索引 * 2 + 1, 右孩子 = 当前节点索引 *2 + 2
从0开始编号,用数组来表示一颗完全二叉树,最后一个非叶子节点索引:(最后一个节点索引-1)/2,
初始化
1 |
|
建堆 核心:heapify O(logN)
heapify:将任意数组整理成堆的形状
优化:如果将个元素逐个插入到一个空堆中,这样建堆 复杂度为O(NlogN),heapify的过程,算法复杂度为O(N)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18// heapify:将任意数组整理成堆的形状 将每个节点都符合最大堆的性质
// 因为叶节点本身没有子节点所以符合最大堆的性质,只需从最后一个非叶子节点到堆顶节点,依次将每个节点堆化
// 注意:heapfiy之后数组中元素并不是从大到小的顺序
MaxHeap *buildHeap(int *arr, int n) {
// 初始化堆 并且 对堆进行赋值
/*** 堆中元素 ∈ [0,size-1] ***/
MaxHeap *heap = (MaxHeap *) malloc(sizeof(MaxHeap));
heap->size = 0;
for (int i = 0; i < n; ++i) {
heap->data[i] = arr[i];
heap->size++;
}
// heapfiy:最后一个节点的索引为size-1,因为数组从0开始,所以最后一个非叶子节点索引(size-1-1)/2
for (int i = (heap->size - 2) / 2; i >= 0; --i) {
shiftDown(heap, i);
}
return heap;
}
插入 核心:shiftUp O(logN)
基本思想:先将节点插入堆中,然后通过shiftUp操作将该节点放在满足最大堆性质的位置shiftUp:将待调整节点与其父节点比较,如果待调整节点比其父节点大,交换两者位置,待调整节点继续与其新父节点比较,如果遇到待调整节点 <= 父亲节点,说明满足最大堆的性质,否则一直执行此过程
1 | void shiftUp(MaxHeap *heap, int idx) { |
删除 核心:shiftDown O(logN)
基本思想:将最后一个元素与堆顶元素互换,此时新的堆顶元素不一定符合最大堆的性质,对其进行shiftDownshiftDown:将当前元素与自己的左右孩子中最大的那个比较,如果比最大的孩子小,交换两者位置,继续与新的左右孩子比较,直到大于等于左右孩子中最大的,此时符合最大堆的性质
1 | // 向最大堆中取出堆顶元素 即堆中的最大元素 O(logN) |
一些其他操作
1 | // 获取最大堆顶元素 即整个堆中最大的元素 |
原地堆排序
基本思想:首先将待排序数组heapfiy,即数组中每个元素都满足最大堆的性质1
2
堆的应用-优先队列
- 优先队列与普通队列的区别?
普通队列:先进先出,后进后出
优先队列:出队顺序和入队顺序无关,和优先级有关
为什么使用优先队列?
动态的选择优先级最高的任务
在N个元素中选出前M个元素,快排,归并等都是NlogN ,使用优先队列NlogM- 优先队列可以用什么实现?
| 入队 | 出队 | |
|---|---|---|
| 普通数组 | O(1) |
O(N) 出队时遍历数组找出优先级最高的 |
| 有序数组 | O(N) 入队时需要遍历一遍数组,插入适合的位置 |
O(1) 优先级从大到小 |
| 堆 | O(logN) 完全二叉树 |
O(logN) 完全二叉树 |